https://www.acmicpc.net/problem/1777

자료구조
- Segment Tree
사용 언어
- Python
시간 복잡도
- $O(10^5 log (10^5))$
풀이
포인트
- BOJ 1849번 풀이와 거의 동일
query함수의 분기 조건이 다르다는 것
Segment Tree
이 문제는 BOJ 1849번과 유사한 유형이다.
1849번은 수열 A[i]가 i 앞에 있는 수 들 중, i보다 큰 수들의 개수이다.
1777번은 수열 A[i]가 i 뒤에 있는 수 들 중, i보다 작은 수들의 개수이다.
두 문제의 차이는 1) A[i]의 정의가 앞, 또는 뒤에 있는 수들과 연관되어 있고 2) 이 수들과 작거나 큰 수들의 개수라는 것이다. 이 두 차이 때문에 두 문제는 아래와 같은 관점에서 풀이 방향성이 달라진다.
- 1849번은 트리를 업데이트하고 쿼리를 진행할 때, A의 앞 원소부터 진행한다. 하지만 1777번은 A의 뒤 원소부터 진행한다.
- 1849번은
query함수에서 if 분기 조건이tree[node*2] > k이다. 하지만 1777번의 if 분기 조건은tree[node*2 + 1] > k이다.
첫 번째 방향성
1777번 문제는 A[i]를 i 뒤에 있는 수 들에서 정의한다. 따라서 원래 순열을 복원할 때, A의 뒤 원소부터 보는게 올바르다. 예제 A = [0,1,0,2,2,1,2,0]을 보며 이해를 해보자.
- A[8] = 0: 8 뒤에 있는 수 들 중, 8보다 작은 수는 0개이다. 따라서 8은 무조건 8번째에 위치해야한다. 왜냐하면 1~7은 모두 8보다 작기 때문이다.
- A[7] = 2: 7 뒤에 있는 수 들 중, 7보다 작은 수는 2개이다. 따라서 7은 무조건 5번째에 위치해야한다. 그래야 6,7번째에 7보다 작은 수 2개가 오기 때문이다. (8번째는 이미 8로 채워졌다.)
- A[6] = 1: 6 뒤에 있는 수 들 중, 6보다 작은 수는 1개이다. 따라서 6은 무조건 6번째에 위치해야한다. 그래야 7번째에 6보다 작은 수 1개가 오기 때문이다. (5, 8번째는 이미 각각 7과 8로 채워졌다.)
단순하게 for 문 풀이로 보자면, A의 뒤쪽 원소부터 접근하는 것이 맞다.
두 번째 방향성
1849번 문제와 마찬가지로 tree[node] 값을 start ~ end번째에 비어 있는 칸의 개수로 정의하자. 초기 트리의 모습은 아래와 같다.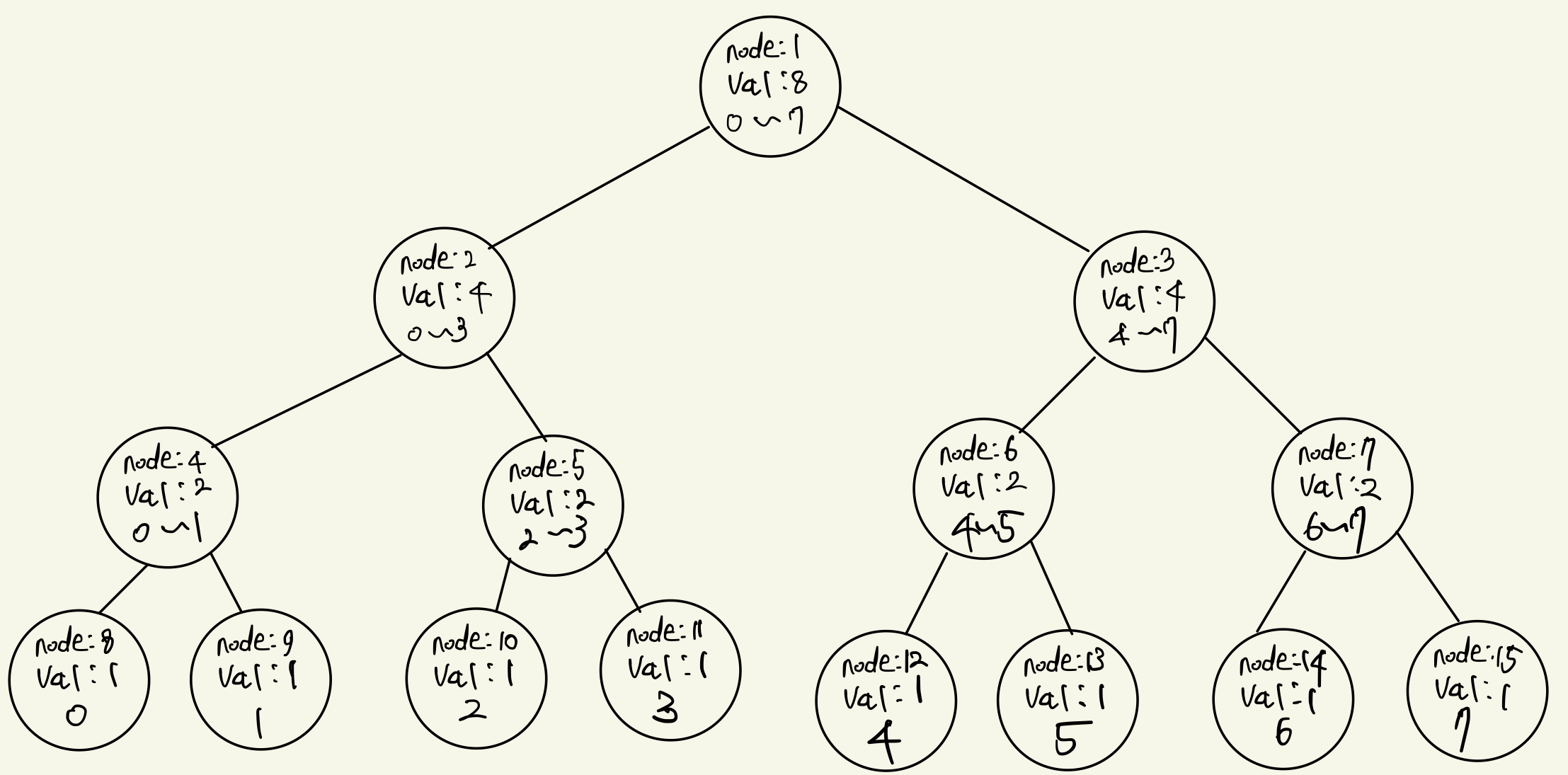
이때 트리의 오른쪽 자식 노드 값과 k를 비교한다. 왜냐하면, A의 뒤 원소부터 살펴볼 것이고 따라서 원래 수열의 뒤쪽부터 원소를 삽입할 것이기 때문이다. 만약 조건을 충족한다면 오른쪽 자식 노드로 함수를 호출한다.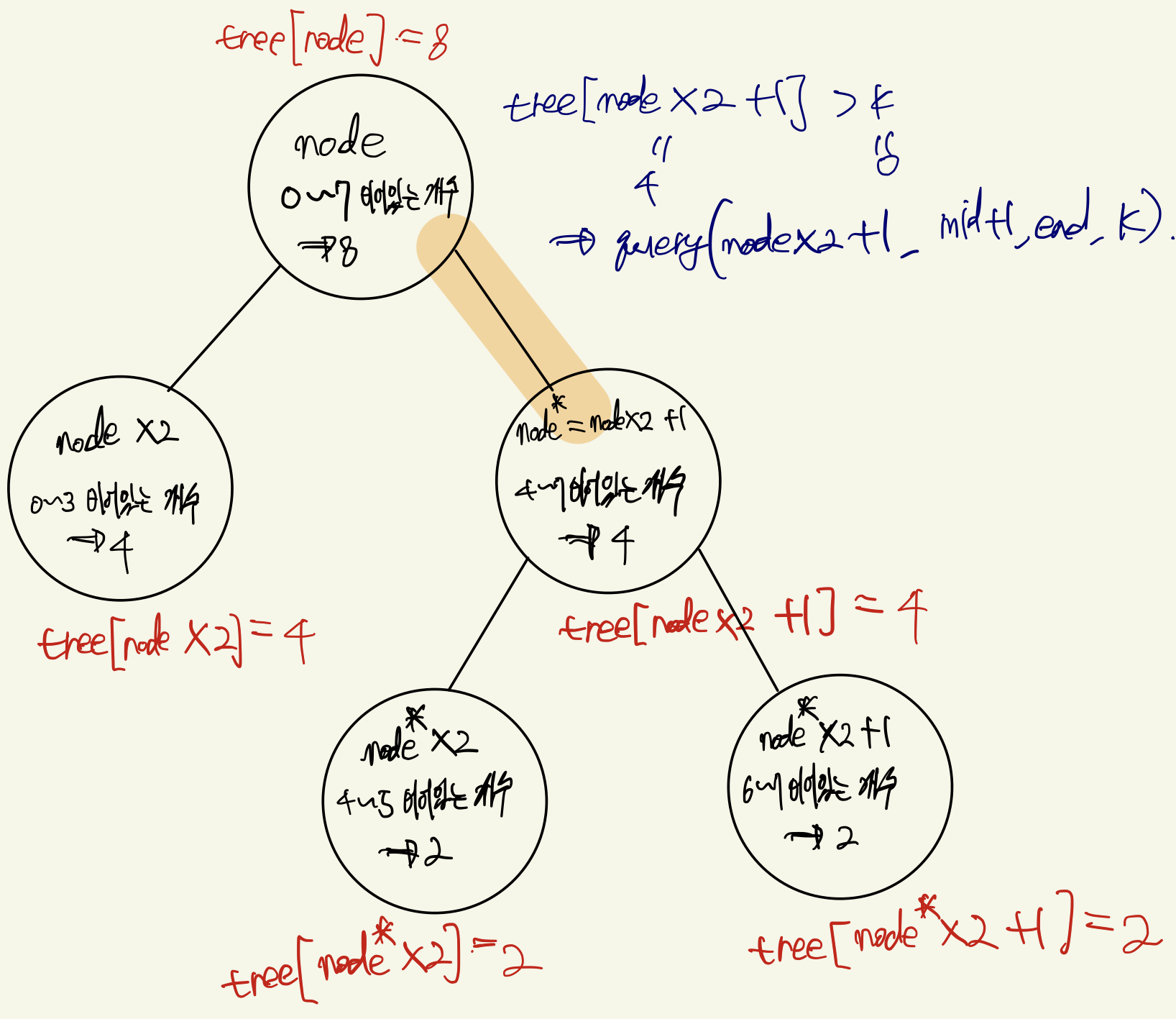
마찬가지로 다음 노드에서도 오른쪽 자식 노드로 함수를 호출한다.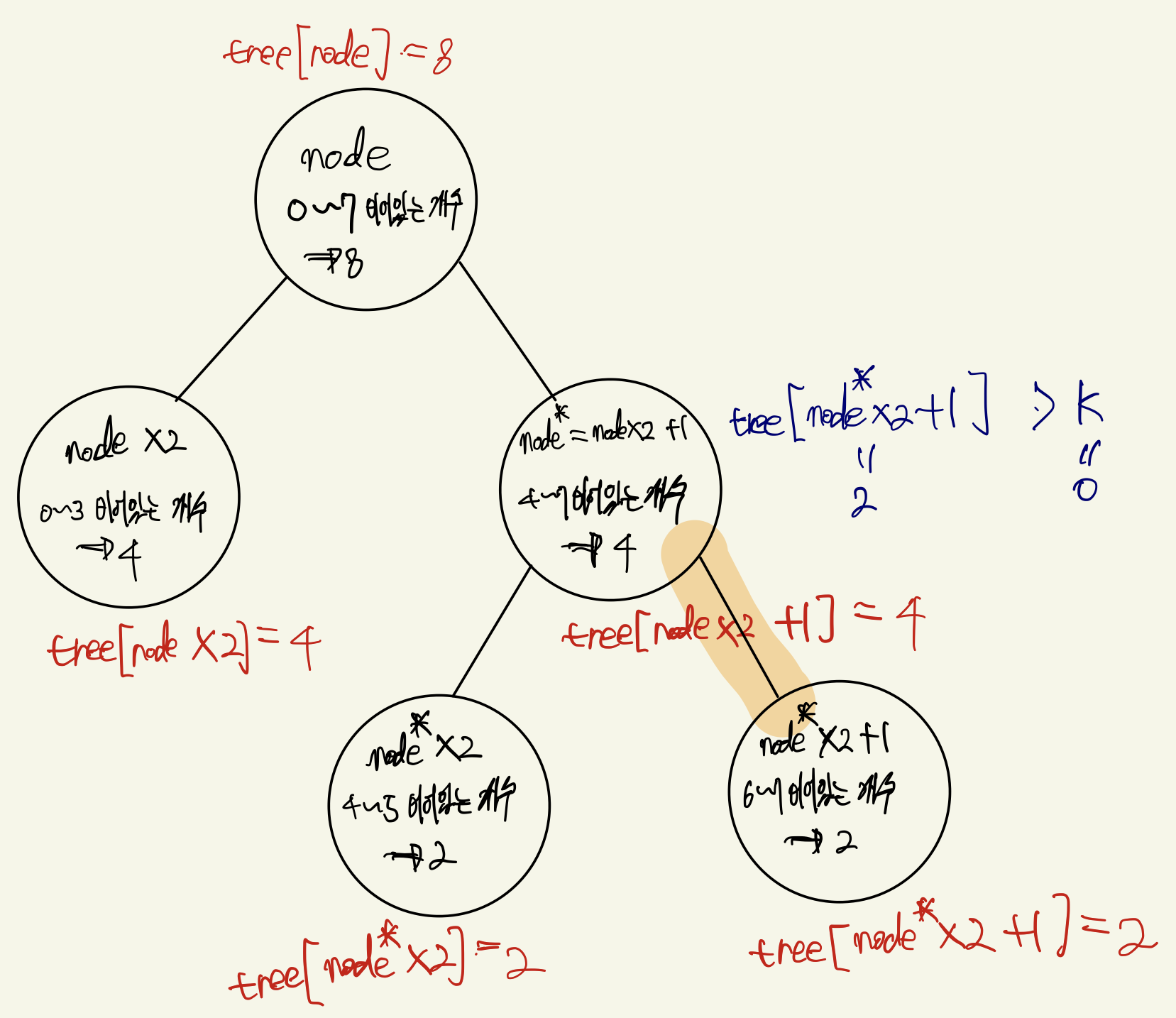
이런 식으로 마지막에는 tree의 마지막 원소에 접근할 것이고, 이는 곧 leaf node이므로, 원래 수열의 마지막 번째에 8을 삽입한다.
쿼리를 진행한 후에는, update 함수를 통해 해당 원소가 삽입된 인덱스를 포함하는 트리의 모든 노드 값을 1씩 빼줘야한다. 왜냐하면, 해당 인덱스에 값이 삽입됐고 따라서 비어있는 수가 1만큼 감소하기 때문이다.
소스코드는 아래와 같다.
[Source Code]
def init(node, start, end):
if start == end:
tree[node] = 1
return tree[node]
tree[node] = init(node*2, start, (start+end)//2) + init(node*2 + 1, (start+end)//2+1, end)
return tree[node]
def query(node, start, end, val):
if start == end:
return start
if val < tree[node*2 + 1]:
return query(node*2 + 1, (start+end)//2 + 1, end, val)
else:
return query(node * 2, start, (start + end) // 2, val - tree[node * 2 + 1])
def update(node, start, end, index):
if not (start <= index <= end):
return
tree[node] -= 1
if start != end:
update(node*2, start, (start+end)//2, index)
update(node*2 + 1, (start+end)//2 + 1, end, index)
n = int(input())
l = list(map(int,input().split()))
tree = [0]*(4*n)
ans = [0]*n
init(1,0,n-1)
for i in range(n-1,-1,-1):
idx = query(1,0,n-1,l[i])
ans[idx] = i+1
update(1,0,n-1,idx)
for i in ans:
print(i, end=' ')'Programming > BOJ' 카테고리의 다른 글
| [segment tree] 11658번 구간 합 구하기 3 (0) | 2022.05.25 |
|---|---|
| [segment tree] 1849번 순열 (0) | 2022.04.09 |
| [segment tree] 2243번 사탕상자 (0) | 2022.04.08 |
| [segment tree] 11505번 구간 곱 구하기 (0) | 2022.03.20 |
| [구현] 2174번 로봇 시뮬레이션 (0) | 2022.03.17 |




댓글