https://www.acmicpc.net/problem/1849

자료구조
- Segment Tree
사용 언어
- Python
시간 복잡도
- $O(10^5log(10^5))$
풀이
포인트
- BOJ 2243번 풀이와 거의 동일
- 두 가지 다른 점은 update 함수를 따로 구현하면 TIL이 발생하여 query 함수에서 이를 처리해줘야 한다는 점과 query 함수에서 분기하는 if 조건이
=을 포함하지 않는다는 점
단순 for문 풀이: TIL
BOJ 2243번 풀이와 마찬가지로 왜 segment tree 자료구조를 사용해야하는지에 대해서 생각해보자. for문을 이용해볼 때, 시간 복잡도가 어떻게 나오는지 살펴본다.
입력에는 수열 A가 주어지고 A[i]는 그 수열에서 i 앞에 있는 수(i 왼쪽에 있는 수 들 중,)들 중, 원래 수열에서 i보다 큰 수의 개수를 의미한다. 수열 A의 입력을 하나씩 받아보면서 원래 수열을 채워본다. 그리고 시간 복잡도를 분석해보자. 예시 입력은 BOJ에서 가져왔다. ( A = [5,0,1,2,1,2,0,0] )
A[1] = 5일 때
원래 수열에서 1 왼쪽에 있는 수들 중, 1보다 큰 수들이 5개라는 뜻이다. 그러면 원래 수열에서 1은 6번째 일수밖에 없다.
A[2] = 0일 때
원래 수열에서 2 왼쪽에 있는 수들 중, 2보다 큰 수들이 0개라는 뜻이다. 그러면 원래 수열에서 2는 1번째 일수밖에 없다.
A[3] = 1일 때
원래 수열에서 3 왼쪽에 있는 수들 중, 3보다 큰 수들이 1개라는 뜻이다. 현재 첫 번째에 3보다 작은 수인 2가 들어가 있다. 그리고 앞으로 살펴볼 수들은 3보다 큰 수들(4 ~ 8)밖에 없다. 따라서 무조건 하나의 공간만을 남겨야하고, 3이 원래 수열에서 3번째에 있다면 2번째에 그 공간을 남길 수 있다. 이 남긴 공간에 3보다 큰 수들(4 ~ 8) 중 하나가 들어가는 것이다.
A[4] = 2일 때
원래 수열에서 4 왼쪽에 있는 수들 중, 4보다 큰 수들이 2개라는 뜻이다. 즉, 수를 채워나갈 때 빈 칸을 2개를 만들어둬야 한다. 따라서 2번째와 4번째에 빈칸을 만들어 두고, 5번째에 4가 들어가면 된다.
A[5] = 1일 때
원래 수열에서 5 왼쪽에 있는 수들 중, 5보다 큰 수들이 1개라는 뜻이다. 즉, 수를 채워나갈 때 빈 칸을 1개 만들어둬야 한다. 따라서 5가 4번째에 들어갔을 때 2번째에 빈칸이 생기므로 4번째에 넣으면 된다.
이런 식으로 쭉 8번째까지 채워나가면 된다. 눈치 챘겠지만, 총 n개의 수가 주어졌을 때, 각 수에 대해서 원래 수열을 선형 시간으로 조회한다. 따라서 단순하게 for 문을 사용할 경우, $O(n^2) = O(10^{10})$의 시간이 소요되어 TIL을 받는다. 따라서 수열을 선형 시간으로 조회하는 부분을 $logn$으로 줄이기 위해 segment tree을 사용해야한다.
Segment Tree
tree[1]의 값을 0 ~ n-1번째까지 채워지지 않은 요소의 개수, tree[2]의 값을 0 ~ mid번째 까지 채워지지 않은 요소의 개수, tree[3]의 값을 mid+1 ~ n-1번째 까지 채워지지 않은 요소의 개수로 나머지 tree 값들도 정의해보자. 원래 수열이 채워지기 전에는 leaf node들은 기본적으로 모두 1의 값을 가지고, 이를 재귀적으로 더해주면 아래와 같은 트리 구조를 도출할 수 있다.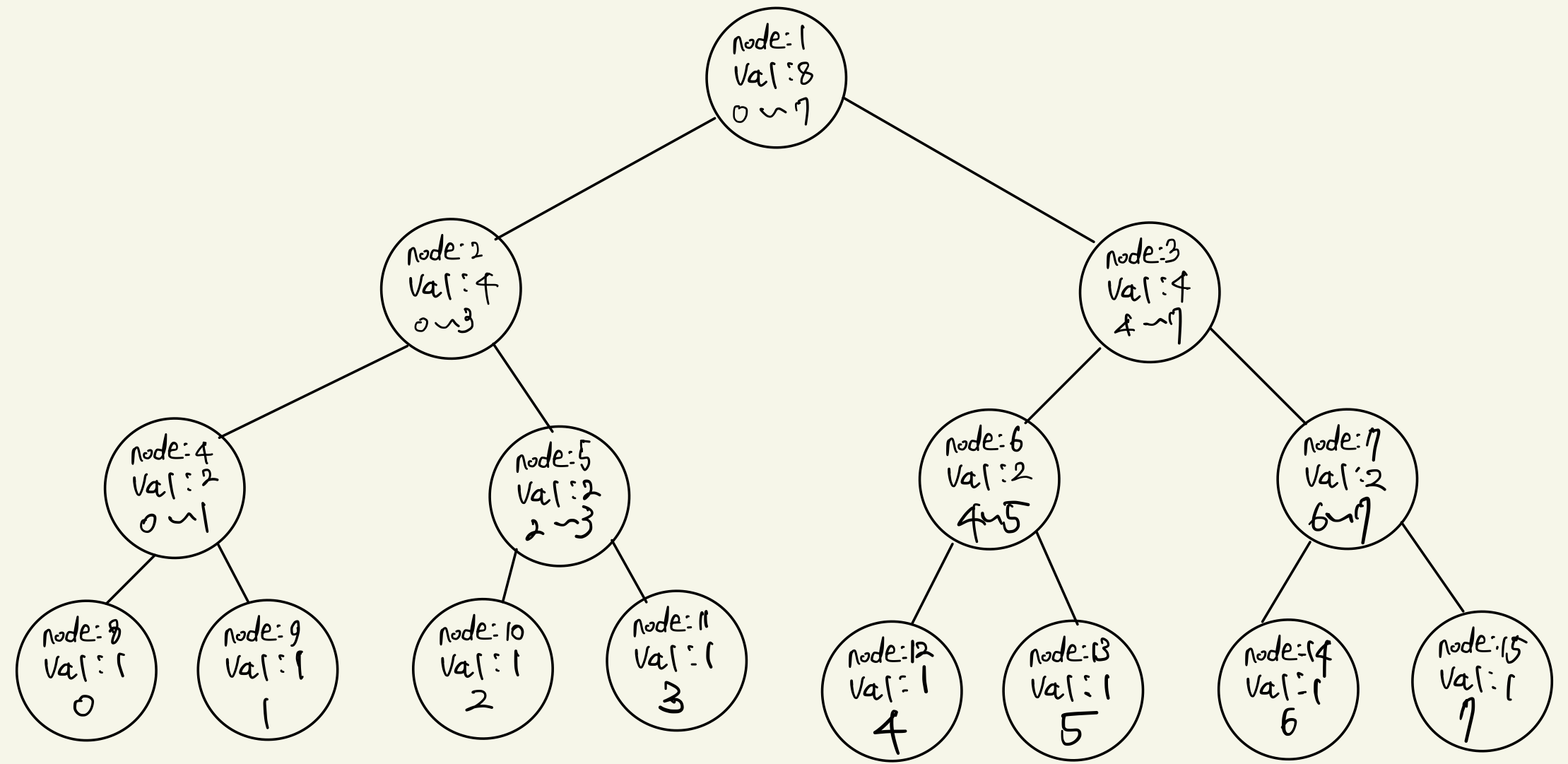
초기 트리 구조이므로, 예를 들어 tree[1]은 8의 값을 가진다. 0 ~ 7번째 까지의 수 중, 초기에는 모두 채워지지 않았으므로 8의 값을 가지는 가지는 것이다.
이제 A[1] = 5을 이용해 원래 수열에서 1을 채우는 과정을 따라가보자. 위 for문 풀이에서는, 원래 수열을 처음부터 방문하며 채워지지 않은 부분의 개수를 하나씩 카운트해서 6번째에 도달했을 때 그 앞에 5개가 채워지지 않았으므로 6번째에 1을 채워넣었다. 하지만 segment tree에서는 이를 $logn$의 시간으로 탐색하는 것이다.
이를 위해 BOJ 2243번 풀이와 동일한 전략을 취한다. 현재 우리가 관심있는 위치는 그 앞에 5개의 채워지지 않은 부분이 있는 곳이다. 그럼 현재노드에서 5와 왼쪽 자식노드의 값(tree[node*2])을 비교해볼 때, tree[node*2]이 5보다 크다면, 왼쪽 자식노드가 커버하는 인덱스에 1이 들어갈 위치가 존재한다는 뜻이다. 왜냐하면, 왼쪽 자식노드가 커버하는 인덱스의 채워지지 않은 부분의 개수가 5보다 크기 때문이다. 따라서 사탕문제와 유사하게 query 함수의 if문을 아래와 같이 구성한다.
if tree[node*2] > k:
return query(node*2, start, (start+end)//2, k)다음으로 살펴볼 경우는 현재 노드에서 tree[node*2]이 5보다 작은 경우이다. 그러면 왼쪽 자식노드가 커버하는 인덱스에 1이 들어갈 위치가 존재하지 않는다는 것이다. 왜냐하면 그곳에서 채워지지 않은 부분의 개수가 5보다 작기 때문이다. 따라서 오른쪽 자식노드가 커버하는 인덱스에 1이 들어갈 위치가 존재함을 알 수있으므로 오른쪽 자식노드를 방문해야한다. 이때 사탕문제와 비슷하게 오른쪽 자식노드에서는 채워지지 않는 부분이 5인 인덱스를 찾는게 아니라 k-tree[node*2]를 찾는다. 이유는 사탕문제와 유사하게, 시작점 (기준점)이 오른쪽 노드가 커버하는 첫번째 인덱스로 바뀌었기 때문에 이를 맞추는 과정이라고 생각하면 된다.
else:
return query(node * 2 + 1, (start + end) // 2 + 1, end, k-tree[node*2])결론적으로 A[1] = 5을 통해 1이 존재하는 인덱스를 찾아가는 과정을 아래 그림과 같이 표현할 수 있다.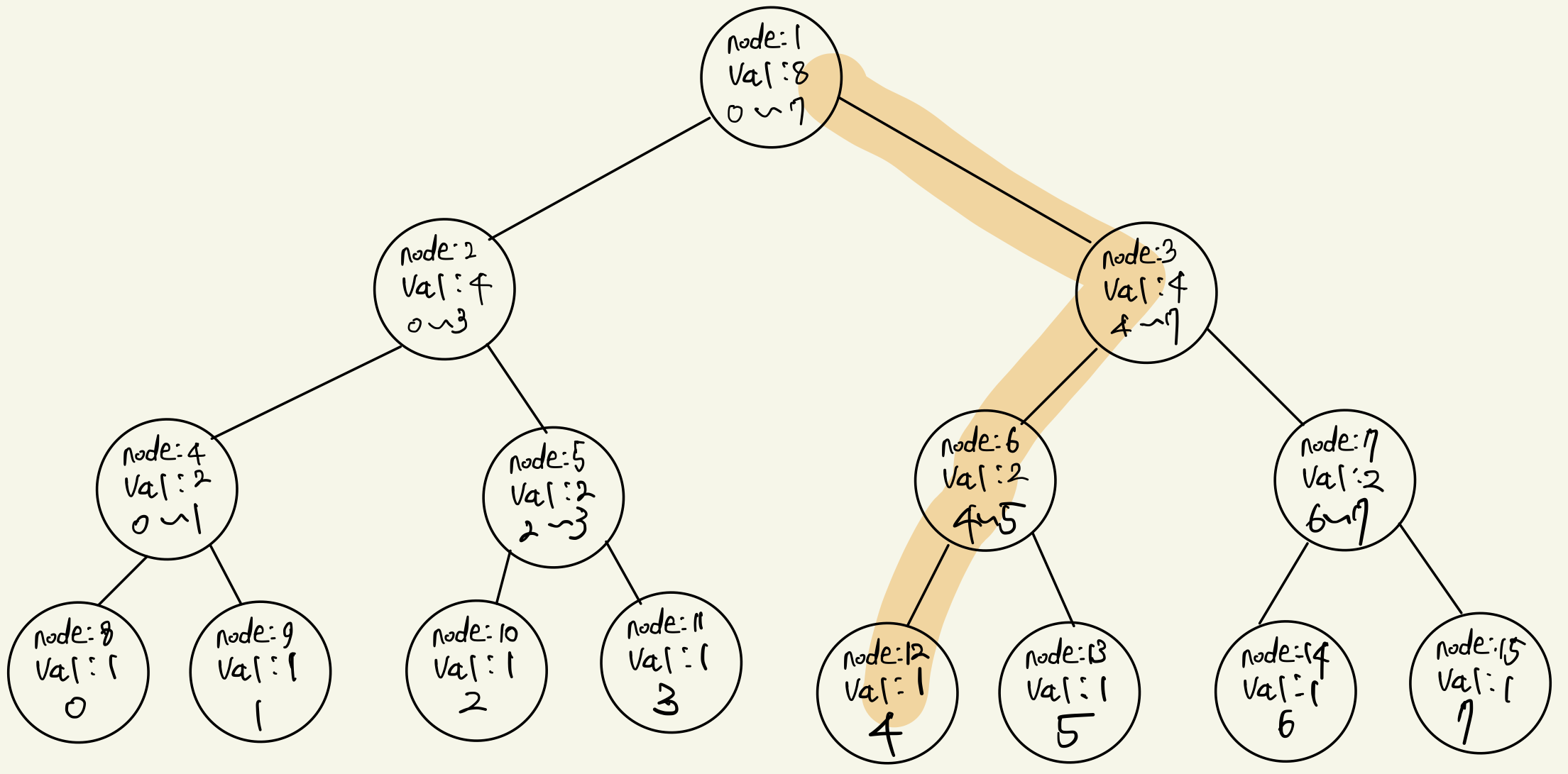
주의할 점
여기서 매우 중요한 포인트가 있다. if문이 =을 포함하지 않는다는 것이다. 그 이유는 무엇일까? A[1] = 4인 경우를 살펴보자. 1 앞에 1보다 큰 수가 4개가 있다. 따라서 1은 5번째에 와야한다.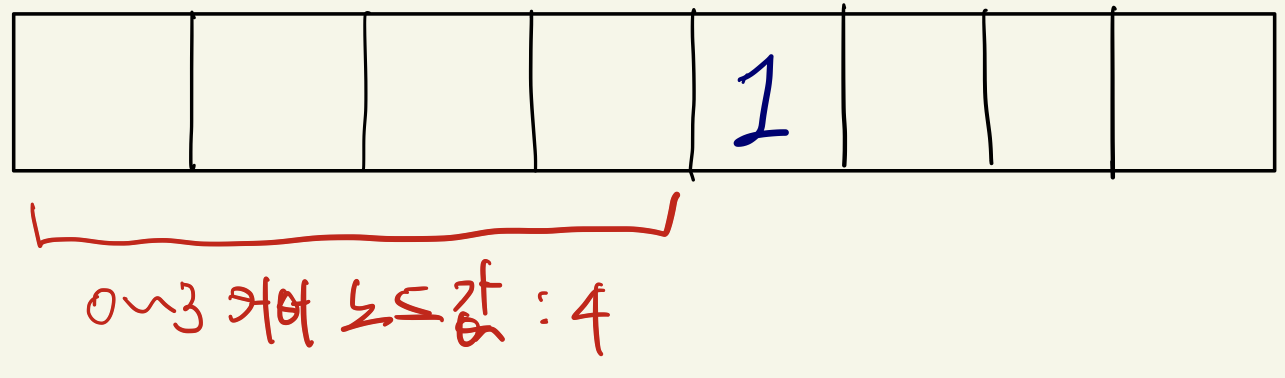
만약 if문이 =을 포함한다면, 재귀 함수가 왼쪽 자식노드를 방문한다. 그러고 최종적으로 4번째 값에 1을 넣으라는 결론을 얻는다.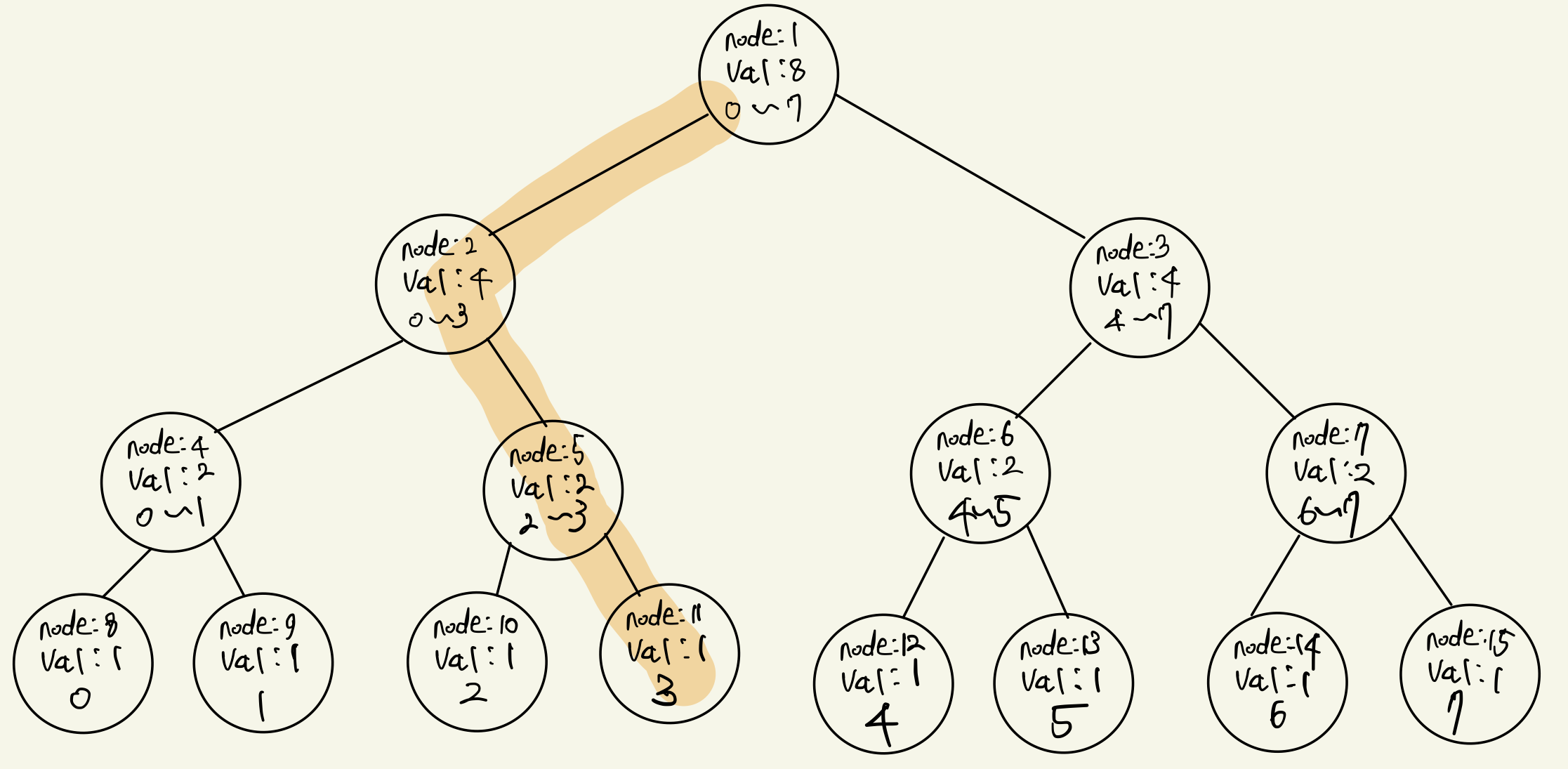
즉, 다시 말해 1 앞에 1보다 큰 수가 3개가 있는 결과를 얻는 것이다. 이 미묘한 차이 때문에 본인은 꽤나 고생했으니 다른 분들은 시간을 낭비하지말고 이해하시길 바란다.
또한 사탕문제와 동일하게 update 함수를 구현하면, TIL을 받는다. 이 부분에 대해서는 솔직히 아직까지 명쾌한 답을 찾지 못했다. 결국 수를 채워넣을 때마다 트리를 업데이트해줘야 하므로, 엄밀하게 시간 복잡도는 $O(10^5(2log(10^5)))$인데, 두 번의 로그 탐색을 했다고 TIL을 받은 것 같다. 따라서 이 문제를 파이썬으로 시간 통과하기 위해서 query 함수를 호출할 때마다 해당 노드의 값을 1씩 빼는 것이다.
tree[node] -= 1이렇게 할 수 있는 이유는, tree의 값이 의미하는게, 그 노드가 커버하는 인덱스 중 채워지지 않은 부분의 개수이고 query가 노드를 방문할 때마다 그 노드가 커버하는 인덱스에서 채워지지 않는 부분의 개수는 1씩 줄어들 것이기 때문이다.
최종 소스코드는 아래와 같다.
[Source Code]
from math import log2, ceil
import sys
input = sys.stdin.readline
def init(node, start, end):
if start == end:
tree[node] = 1
return tree[node]
tree[node] = init(node*2, start, (start+end)//2) + init(node*2 + 1, (start+end)//2+1, end)
return tree[node]
def query(node, start, end, k):
tree[node] -= 1
if start == end:
# print(start+1)
return start
if tree[node*2] > k:
return query(node*2, start, (start+end)//2, k)
else:
return query(node * 2 + 1, (start + end) // 2 + 1, end, k-tree[node*2])
def update(node, start, end, index, diff=-1):
if not (start <= index <= end):
return
tree[node] += diff
if start != end:
update(node*2, start, (start+end)//2, index, diff)
update(node*2 + 1, (start+end)//2 + 1, end, index, diff)
n = int(input())
tree = [0]*(4*n)
tree_size = len(tree)
l = [0]*(n)
init(1,0,n-1)
for i in range(1,n+1):
k = int(input())
x = query(1,0,n-1,k)
l[x] = str(i)
# update(1,0,n-1,x)
print('\n'.join(l))'Programming > BOJ' 카테고리의 다른 글
| [segment tree] 11658번 구간 합 구하기 3 (0) | 2022.05.25 |
|---|---|
| [segment tree] 1777번 순열복원 (0) | 2022.04.24 |
| [segment tree] 2243번 사탕상자 (0) | 2022.04.08 |
| [segment tree] 11505번 구간 곱 구하기 (0) | 2022.03.20 |
| [구현] 2174번 로봇 시뮬레이션 (0) | 2022.03.17 |




댓글