저번 포스팅에서는 numpy을 사용하여 mlp을 구현해보았다.
https://steady-programming.tistory.com/88
[DL][Implementation] Numpy을 사용하여 MLP 구현하기
backpropagation을 수식으로 공부하다가, pytorch로 쓱 하고 지나갈 개념이 아닌 것 같다는 생각이 들었다. 모든 딥러닝 문제에서는 gradient descent을 사용해서 optimal parameter을 찾고 그 과정에서 backpropagat
steady-programming.tistory.com
linear layer에서 weight, bias의 backpropagation을 직접 구현해보며 이해도를 높일 수 있었다. 이번 포스팅에서는 convolution neural networks을 numpy을 사용하여 구현하기 위한 첫번째 단계로 convolution에서 backpropagation은 어떻게 계산되는지 직접 유도해보고 코드로 구현해본다.
What is convolution?
딥러닝에서 convolution 연산은 보통 2차원 이상의 데이터에 대해 kernel(weight)을 정의하고 kernel을 이동하며 matrixwise 곱셈을 하는 것을 의미한다. 이미지 데이터를 예시로 생각해보자. 색깔이 있는 이미지는 Channel x H x W로 데이터가 구성되고, 보통 channel의 수는 3이다. (흑백 이미지의 channel 수는 1이다)
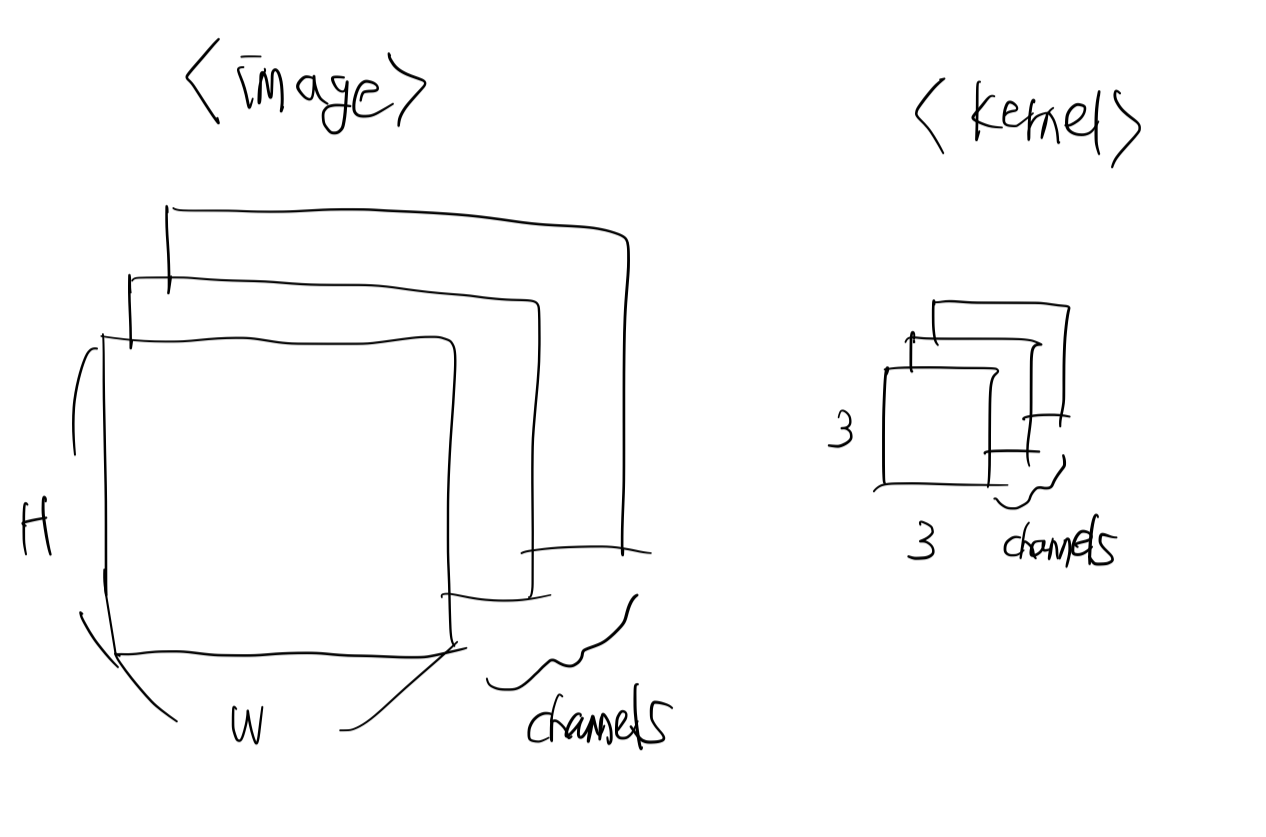
보통 kernel의 높이와 너비는 3으로 정의한다. 이유는 자세히 모르겠지만 일종의 관례인 듯 하다. 구체적인 수식으로 살펴보기 위해 아래와 같이 channel의 수가 1인 경우를 생각해보자.
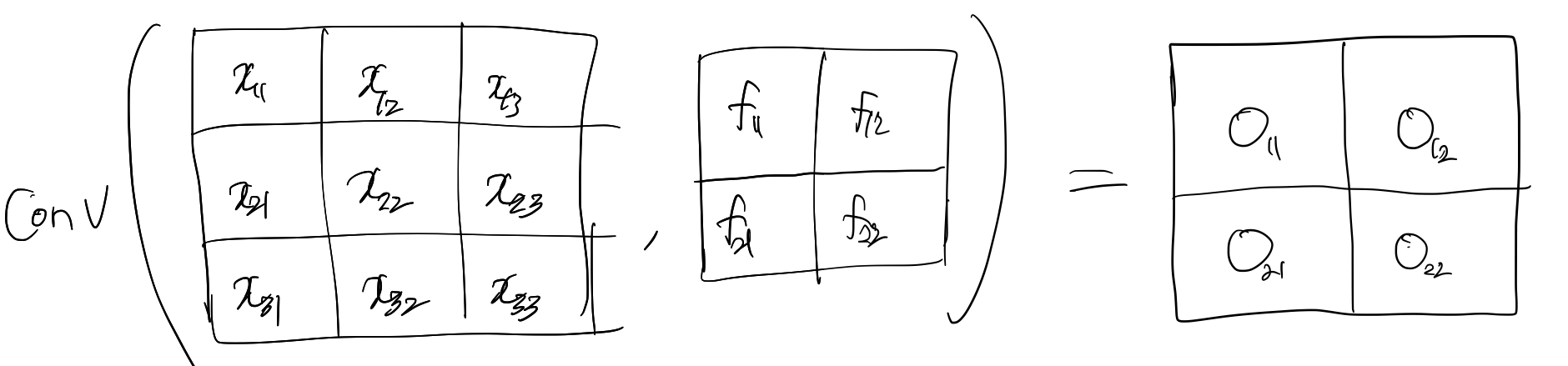
3 x 3 데이터에 2 x 2 kernel을 적용하여 2 x 2 차원의 출력값을 생성하는 과정에 대해 생각해보자. $O_{11}, \cdots, O_{22}$는 아래와 같이 정의된다.
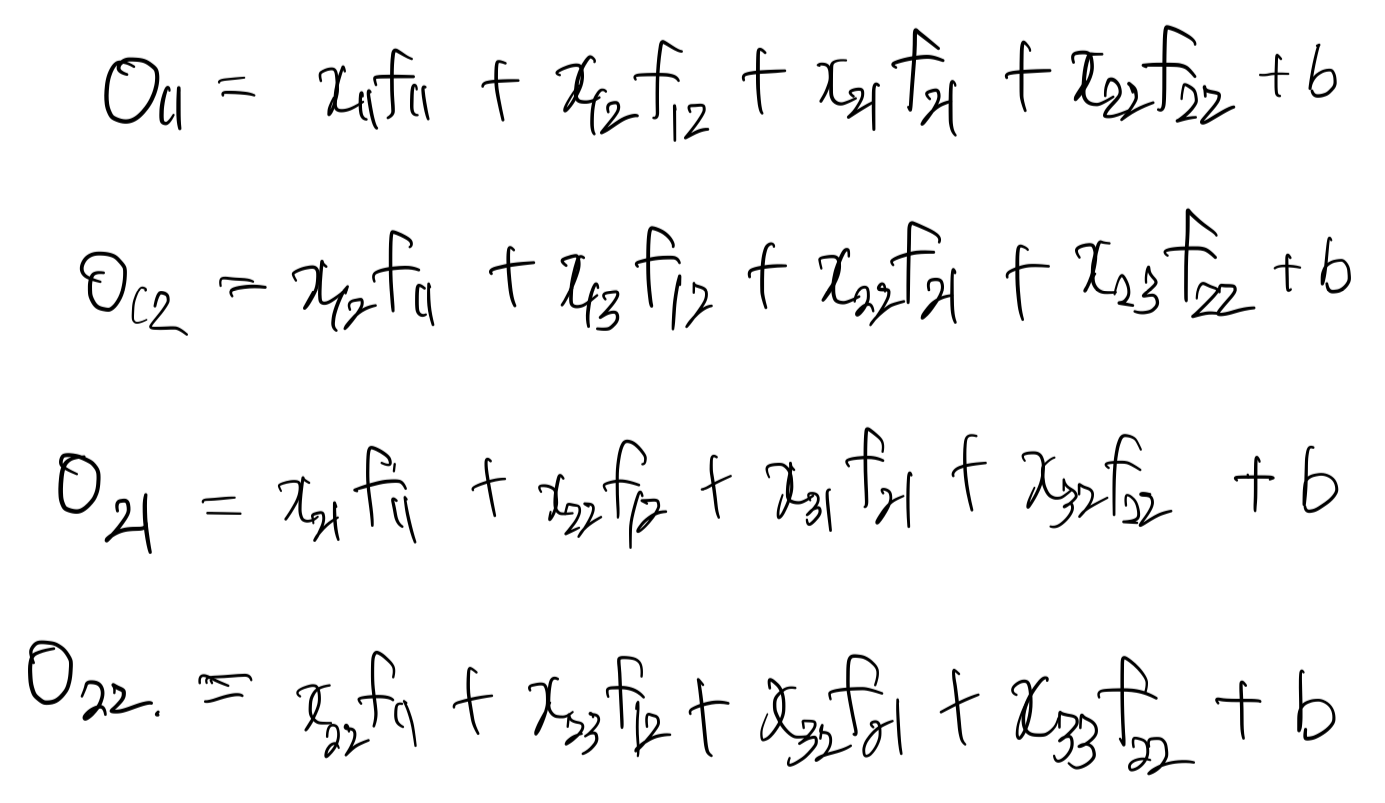
위 수식은 forward 결과 값이다. 학습해야하는 모델 가중치는 $f_{11}, \cdots, f_{22}, b$ 임을 확인할 수 있다. 먼저 convolution 레이어의 기초가 되는 convolve 함수를 구현해보자. (코드는 여기서 확인할 수 있다.)
import numpy as np
def convolve(img, kernel, bias=0, stride=1, full=False):
"""
params
------
img: np.ndarray
dimension (h_in, w_in). one image input assuming no channel
kernel: np.ndarray
dimension (h_k, w_k)
"""
if full == True and stride != 1:
raise ValueError(f"Stride value of full convolution should be equal to 1, got {stride}")
k, _ = kernel.shape
if full:
img = np.pad(img, pad_width=((k-1,k-1), (k-1,k-1)))
h_in, w_in = img.shape
h_out, w_out = h_in-k+1, w_in-k+1
out = np.zeros((h_out, w_out))
for i in range(h_out):
for j in range(w_out):
out[i, j] = (img[i:i + k, j:j + k] * kernel).sum() + bias
return out
full convolution 여부에 따라서 이미지를 padding 해주고 convolution 연산을 수행한다. 해당 연산을 convolution 레이어에서 정의한게 아니라 따로 함수로 빼둔 이유는 gradient을 구하는 과정에서 convolution 연산이 다시 사용되기 때문이다. backpropagation을 살펴보기 전에 forward propagation을 먼저 정의해보자. (코드는 여기서 확인할 수 있다.)
import numpy as np
from modules.base import BaseModule
from tools.utils import convolve
class Convolution(BaseModule):
def __init__(self, input_dim, kernel_dim: tuple , padding: str):
super().__init__()
n, h_in, w_in = input_dim
self.padding = padding
self.kernel = np.random.uniform(-0.1,0.1,kernel_dim)
self.b = np.random.uniform(-0.1,0.1,1)
# self.kernel = np.round(self.kernel, 4)
# self.b = np.round(self.b, 4)
h_out, w_out = self.calculate_out_dims(h_in, w_in)
self.h_out = h_out
self.w_out = w_out
self.dk = None
self.db = None
def forward(self, imgs):
"""
params
------
imgs: np.ndarray
dimension (n, h_in, w_in). 3d array input.
"""
n, h_in, w_in = imgs.shape
pad = self.calculate_pad_dims()
out = np.zeros((n, self.h_out, self.w_out))
imgs = np.pad(imgs, pad_width=((0,0),(pad[0], pad[0]), (pad[1], pad[1])))
self.X = imgs
for i, img in enumerate(imgs):
out[i] = convolve(img, self.kernel, self.b)
return out
def backward(self, dx_out):
...
def calculate_pad_dims(self):
if self.padding == "same":
h_f, w_f = self.kernel.shape
return (h_f - 1) // 2, (w_f - 1) // 2
elif self.padding == "valid":
return 0, 0
else:
raise
def calculate_out_dims(self, h_in, w_in):
k, _ = self.kernel.shape
if self.padding == "same":
return h_in, w_in
elif self.padding == "valid":
return h_in-k+1, w_in-k+1
else:
raise
def get_params_grad(self):
...
padding 값이 `same`인지, `valid`인지 여부에 따라서 padding의 크기와 output의 차원이 정해진다. 이를 `calculate_pad_dims` 메써드와 `calculate_out_dims`에서 확인할 수 있다. `forward` 메써드에는 이전에 작성한 `convolve` 함수를 통해 이미지와 kernel 간에 convolution 연산을 진행한다.
Backpropagation in convolution
convolution 연산은 아래와 같이 정의됨을 위에서 확인했다.
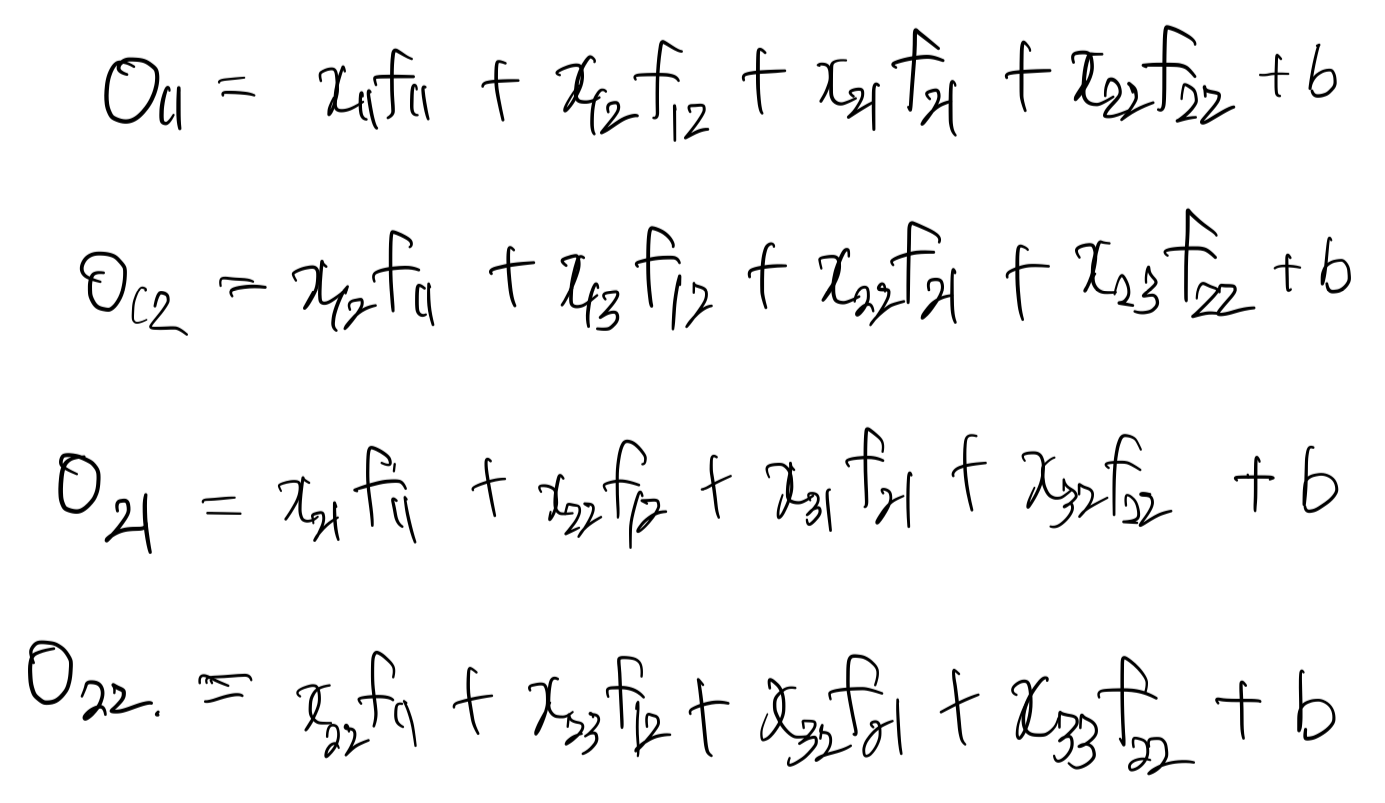
여기서 모델 가중치는 $f_{11}, \cdots, f_{22}, b$ 이므로 이에 대한 gradients을 구하면 된다. 아래를 살펴보자.

upstream gradient인 $\dfrac{\partial L}{\partial O_{ij}}$와 함께 계산된다. 근데 잘 살펴보면, upstream gradient와 입력 데이터간에 convolution임을 눈치챌 수 있다.
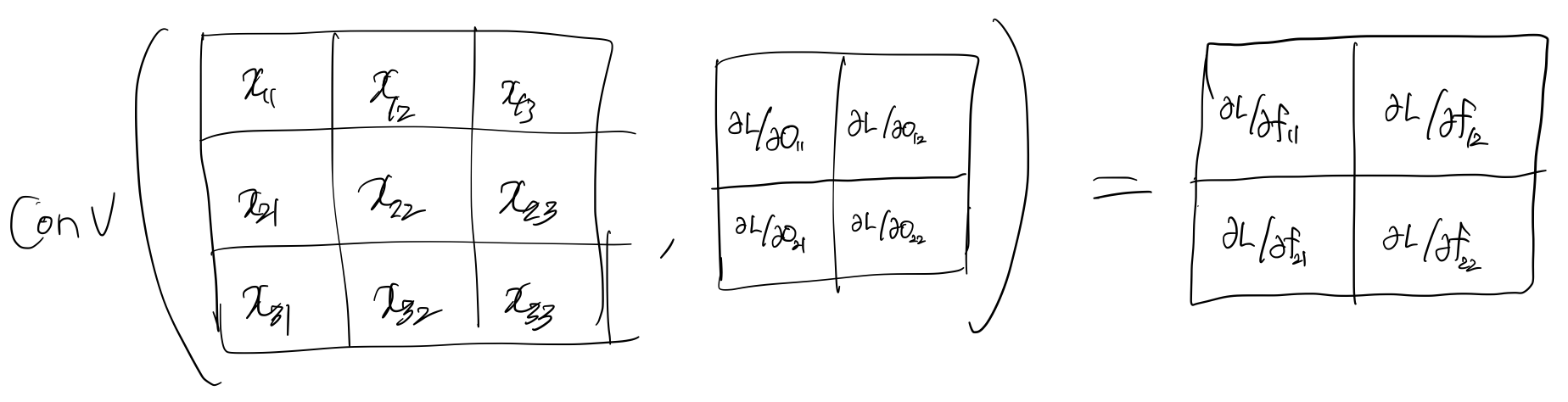
신기하다 ㅎㅎ kernel의 gradient가 결국은 또 다른 convolution의 결과라니..
이제 다음으로 downstream gradient을 구하기 위해 $\dfrac{\partial L}{\partial x}$을 구해보자.
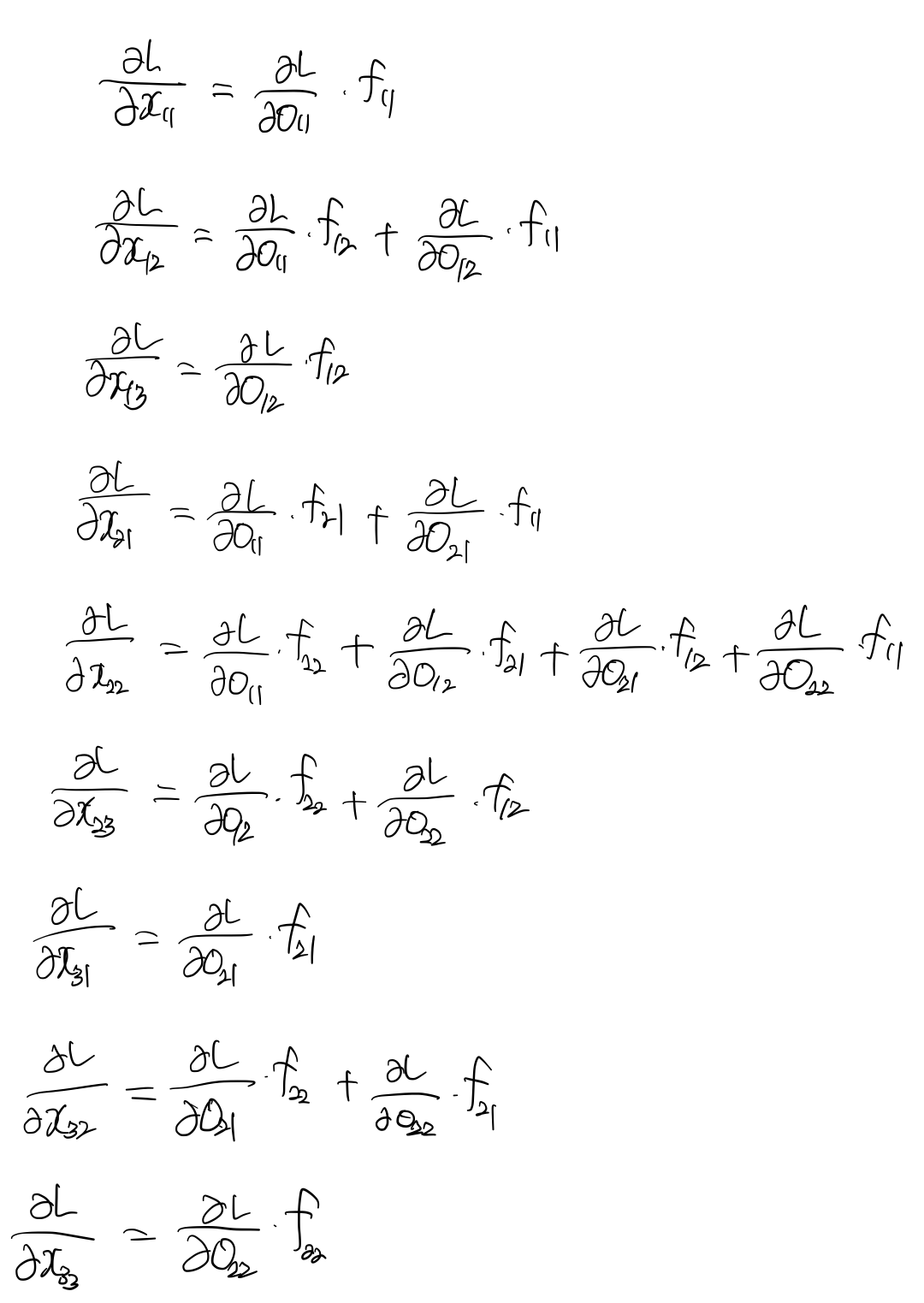
얼핏보기에는 불규칙해보이지만 이는 upstream gradient와 180도 회전한 kernel 간의 full convolution 이다. 여기서 upstream gradient을 180도 회전하고 kernel과 convolution을 하든, upstream gradient은 그대로 두고 kernel을 180도로 회전해서 convolution을 하든, 결과는 동일하다.
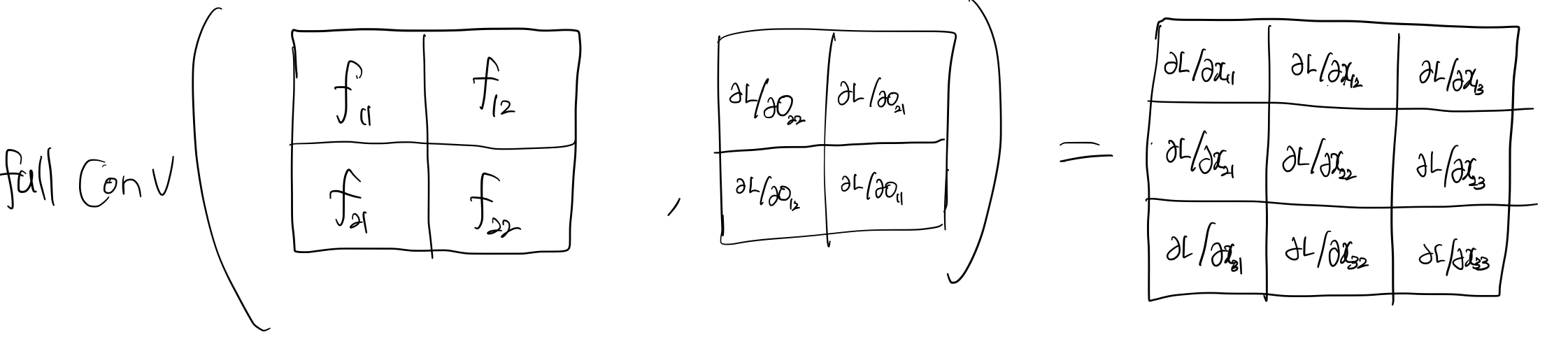
정리하면 아래와 같다.
- kernel의 gradient: 입력 이미지와 upstream gradient간의 convolution
- downstream gradient: upstream gradient와 180도 회전한 kernel 간의 full convolution
이제 backward 메써드를 살펴보자.
import numpy as np
from modules.base import BaseModule
from tools.utils import convolve
class Convolution(BaseModule):
def __init__(self, input_dim, kernel_dim: tuple , padding: str):
...
def forward(self, imgs):
...
def backward(self, dx_out):
"""
params
------
dx_out: np.ndarray (n, h_out, w_out)
Upstream gradients from loss function.
return
------
dX: np.ndarray(n, h_in, w_in)
Gradients of current input, which is
full convolution btw 180 degree rotated kernel and upstream gradients
"""
dx_in = np.zeros_like(self.X)
n, h_in, w_in = dx_in.shape
dk = np.zeros_like(self.kernel)
db = dx_out.sum()
for img, dX_out_i in zip(self.X, dx_out):
dk += convolve(img, dX_out_i)
rotate_kernel = np.rot90(self.kernel, k=2)
for i in range(n):
dx_in[i] = convolve(dx_out[i], rotate_kernel, full=True)
self.dk = dk
self.db = db
return dx_in
`convolve` 함수를 미리 정의해서 사실 그렇게 복잡하지는 않다. 한가지 주의하자면, 각 이미지에서 계산되는 kernel에 대한 gradient을 `dk`에 더해줘야한다는 것이다.
Conclusion
이로써 convolution layer의 forward / backward 메써드를 모두 구현해봤다. convolution은 forward propa만 할줄 알았는데 gradient을 직접 구해봄으로써 어떻게 gradient가 흘러가는지 확실히 알 수 있었다. 다음 포스팅에서는 이 모듈을 사용하여 간단한 CNN을 구성해보고 pytorch의 결과와 직접 비교해보겠다.
Reference
'ML&DL > Basics' 카테고리의 다른 글
| [DL][Implementation] Numpy을 사용하여 CNN 구현하기 (0) | 2024.08.31 |
|---|---|
| [ML / DL] Backpropagation in softmax function (1) | 2024.08.31 |
| [ML / DL] Cross entropy loss function in classification problem (12) | 2024.07.24 |
| [DL][Implementation] Numpy을 사용하여 MLP 구현하기 (1) | 2024.07.13 |
| [DL / Paper review] Auto-Encoding Variational Bayes (2) | 2023.05.06 |




댓글