backpropagation을 수식으로 공부하다가, pytorch로 쓱 하고 지나갈 개념이 아닌 것 같다는 생각이 들었다. 모든 딥러닝 문제에서는 gradient descent을 사용해서 optimal parameter을 찾고 그 과정에서 backpropagation은 반드시 들어가기 때문이다. 물론, pytorch에서 똑똑하신 분들이 성능 좋은 함수들을 구현해주셨으나, 이를 마음껏 활용하기 이전에 직접 backpropagation을 구현해서 도대체 어떻게 돌아가는지 피부로 직접 느껴보고 싶었다.
Model architecture
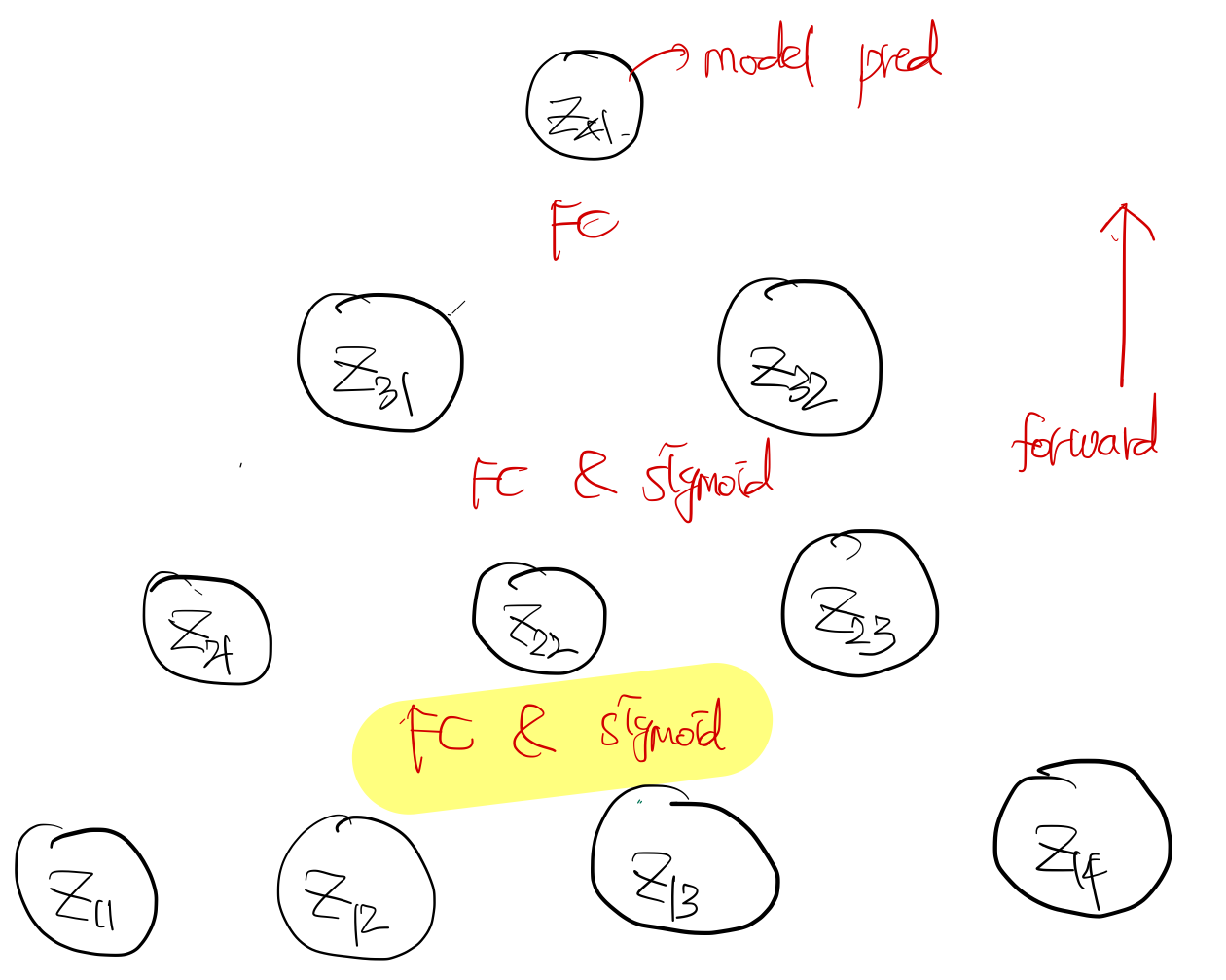
입력 차원은 4, hidden layer의 개수는 3, 깊어질수록 hidden node의 수는 1씩 줄어들도록 모델을 설계해보자. 그림으로 그려보면 아래와 같다.

activation을 넣기 전, 후의 notation은 $z_{ii}, a_{ii}$로 정의한다. 첫번째, 두번째 레이어에서는 Fully connected layer + sigmoid activation function을, 세번째 레이어에서는 FC layer만 적용한다.
Forward pass
backpropagation을 하기 위해서는 반드시 forward pass을 해야한다. 즉, 설계한 모델 아키텍쳐에 따라서 입력값을 통과시키며 출력값을 만들어야한다는 것이다. 그 이유는, backpropagation을 계산하는데, 중간 레이어의 activation 값이 포함되기 때문이다. 먼저, forward pass을 직접 손으로 구해보자.

notation은 아래와 같다.
- $z_{ij}$: $i$번째 레이어의 $j$번째 노드 값
- $a_{ij}$: $i$번째 레이어의 $j$번째 노드 값을 activation에 통과시킨 값. 즉, $f(z_{ij})$.
- $w^{k}_{ij}$: $k$번째 hidden 레이어에서 $z_{k+1,i}$와 $z_{k,j}$간에 연결된 가중치
- $b^{k}_{i}$: $k$번째 hidden 레이어에서 $z_{k+1,i}$과 연결된 bias
notation의 아래첨자가 좀 복잡할 수도 있는데, 그림을 보면 이해가 쉬울 것이다. 여기서 주목해야할점은, 1) 첫번째 레이어에서 입력으로 들어오는 값은 활성함수를 통과한 값이 아니라 입력값 그대로($z_{ij}$)를 받고 두번째, 세번재 레이어에서는 활섬함수를 통과한 값($a_{ij}$)을 받는 다는 점, 2) 세번째 레이어의 출력값은 활성함수를 통과하지 않는다는 점이다. 이 두 사실을 기억해야 backpropagation을 올바르게 구현할 수 있다.
여기까지의 내용을 코드로 살펴보자. 우선 $y, X$ 데이터를 정의한다.
import numpy as np
np.random.seed(1)
n = 1000
k = 10
X = np.random.randn(n,k)
y = np.cos(X).sum(axis=1)
데이터의 총 개수는 1000, 입력 변수의 차원은 10으로 가정한다. $y, x$의 true 관계는 $y = \sum^{10}_{k=1} cosine(x_k)$이다. 비선형 관계이므로 linear model로 문제를 풀 수 없고 neural network 모델을 사용하는 것이다.
다음으로 loss function, sigmoid function, linear network을 아래와 같이 정의하자.
import numpy as np
class Sigmoid:
def __init__(self):
pass
def forward(self, x):
return 1 / (1 + np.exp(-x))
def mean_squared_error(y, pred):
# shape of y, pred: (num_of_data, 1)
return np.square(y - pred).sum() / 2
class Linear:
def __init__(self, input_dim, output_dim):
self.input_dim = input_dim
self.output_dim = output_dim
self.weight = np.random.normal(0, 0.5, (input_dim, output_dim))
self.bias = np.random.normal(0, 0.5, output_dim)
self.weight_grad = None
self.bias_grad = None
def forward(self, x):
# shape of x: (num_of_data, input_dim)
assert x.shape[1] == self.input_dim
x = np.dot(x, self.weight) + self.bias.reshape(1, self.output_dim)
return x # shape: (num_of_data, output_dim)
잘 생각해보면, linear network의 weight matrix는 (input_dim, output_dim)의 차원을 가진다. 그래야 $\mathbb{X}W$로 행렬곱을 했을 때, $(n, output_dim)$ 차원의 행렬이 나오기 때문이다. gradient을 구할 것이므로 `weight_grad`와 `bias_grad`로 변수를 미리 지정해두자.
다음으로 세개의 레이어를 가지는 neural network을 정의해보자.
from abc import abstractmethod
class BaseNeuralNet:
def __init__(self):
pass
@abstractmethod
def forward(self, x):
pass
@abstractmethod
def backward(self, y, pred, X):
pass
@abstractmethod
def step(self, lr):
pass
@abstractmethod
def zero_grad(self):
pass
class NeuralNetwork(BaseNeuralNet):
def __init__(self, struct, n):
super().__init__()
self.struct = struct
self.n = n
self.layers = []
for i in range(1, len(struct)):
self.layers.append( Linear(struct[i-1], struct[i]) )
if i != len(struct)-1:
self.layers.append( Sigmoid() )
def forward(self, x):
self.activated_val = [x]
for layer in self.layers:
x = layer.forward(x)
if layer.__class__.__name__ == "Sigmoid":
self.activated_val.append(x)
return x
def backward(self, y, pred, X):
step = 1
delta = (pred - y)
for layer in self.layers[::-1]:
if layer.__class__.__name__ != "Linear":
continue
activated = self.activated_val[-step]
layer.bias_grad = delta.sum(axis=0) # columnwise sum
layer.weight_grad = np.dot(activated.T, delta) # when initial layer, activated value is equal to input matrix, e.g., X
delta = np.dot(delta, layer.weight.T) * (activated) * (1 - activated)
step += 1
def step(self, lr):
for layer in self.layers:
if layer.__class__.__name__ == "Linear":
layer.weight -= lr * layer.weight_grad
layer.bias -= lr * layer.bias_grad
def zero_grad(self):
for layer in self.layers:
if layer.__class__.__name__ == "Linear":
layer.weight_grad = None
layer.bias_grad = None
`BaseNeuralNet` 클래스를 통해 클래스의 기본 틀을 설계한다. 앞으로 mlp뿐만 아니라 cnn, lstm 등도 구현해볼 예정인데 이때 해당 base class을 사용할 것이다. `struct` argument는 입력부터 출력까지 hidden layer의 node 수를 나타낸다. 본 문제에서 피쳐는 4, 출력값 차원은 1이며 중간의 2개의 hidden layer가 각각 3개, 2개의 노드를 가진다고 하면 `struct=[4,3,2,1]`로 지정하면 된다.
`forward` 메써드에는 FC, Activation의 과정이 표현되어 있다. 입력값이 들어오면 `Linear.forward`와 sigmoid 활섬함수를 차례로 통과시켜준다. 주의할 점은 활성함수를 통과한 값을 `self.activated_val`에 반드시 저장해야한다는 것이다. 활성함수값은 backpropagation에서 사용될 예정이다.
Backpropagation
gradient을 구하는 방법에는 아래 세가지 방법이 있다.
- batch gradient descent: gradient을 구할 때, 한번에 모든 데이터를 사용하는 방법. 데이터의 크기가 커진다면 연산 비용이 많이 발생한다.
- stochastic gradient descent: gradient을 구할 때, 하나의 데이터를 사용하는 방법. 수렴하는데 오래 걸린다.
- mini batch gradient descent: 위 두 방법의 중간 방법으로, 데이터를 여러개의 mini batch로 자르고, 각 mini batch를 사용하여 gradient을 업데이트 한다.
본 포스팅에서는 데이터의 개수가 많지 않으므로 batch gradient descent 방법을 사용하여 gradient을 구해본다. 먼저, loss function은 아래와 같다.
\[ L = \dfrac{1}{2} \sum^n_{i=1} ( y_i - \hat{y}_i )^2 = \dfrac{1}{2} \sum^n_{i=1} ( y_i - z^{(i)}_{41} )^2 \]
batch gradient descent이기 때문에 한번 gradient을 업데이트할 때 모든 데이터를 사용한다. 따라서 summation의 윗첨자가 $n$이 된다.
backpropagation이기 때문에 말 그대로 마지막 레이어에서부터 gradient을 계산한다.
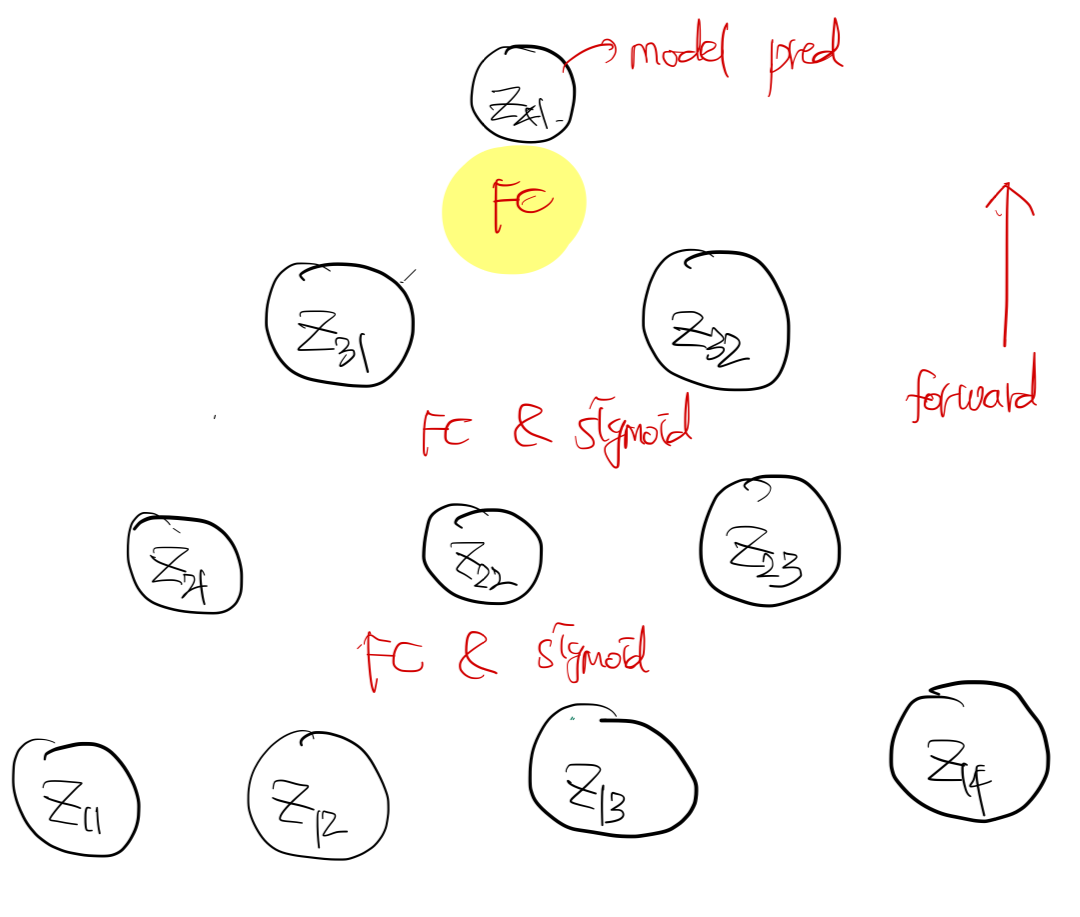
그림으로 보면, 세번째 Linear layer에 대한 gradient을 구하는 것이다. 먼저, $\dfrac{\partial L}{\partial z_{41}}$을 유도해보자.
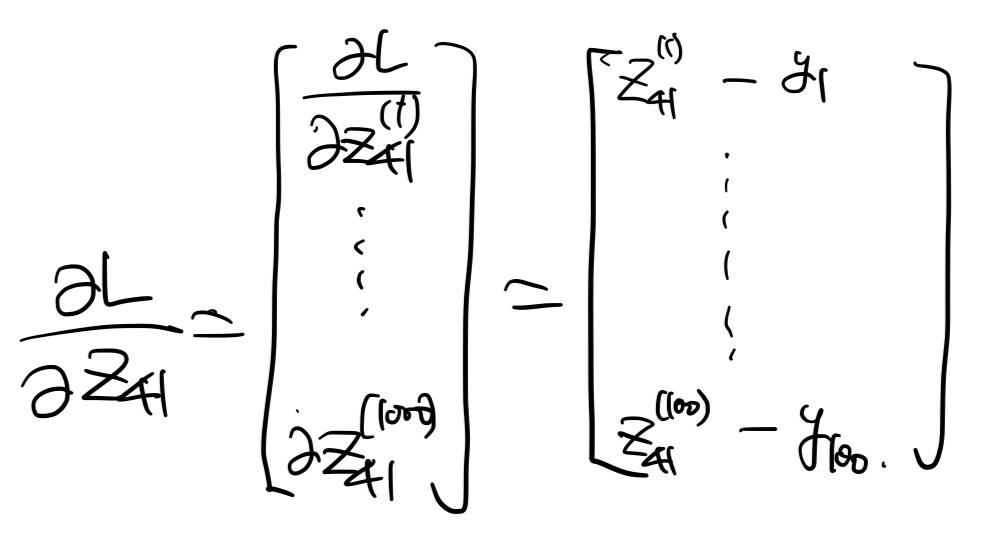
batch gradient descent이기 때문에 1000개의 데이터에 대한 gradient vector을 구한다. 다음으로 $(z_{31}, z_{32} \rightarrow z_{41})$로 가는 FC의 weight, bias에 대한 gradient을 구하기 전에 두 노드의 관계를 다시 한번 짚고 넘어가자.
\[ z^{(i)}_{41} = w^3_{11} a^{(i)}_{31} + w^3_{12} a^{(i)}_{31} + b^3_1 \]
여기서 $a_{ij} = f(z_{ij})$는 $z_{ij}$을 activation function에 통과한 값이다.
$w, b$의 윗첨자는 세번째 레이어임을, $z,a$의 윗첨자는 $i$번째 데이터임을 의미한다. 잘 생각해보면, 세번째 레이어의 weight는 2개, bias는 1개이므로 각각 $(2 \times 1), (1 \times 1)$ 차원의 벡터가 나와야함을 유추해볼 수 있다. 이를 바탕으로 gradient을 구해보면 아래와 같다.

여기서 주목해야할점은 gradient을 계산하는데 activation 값이 들어간다는 것이다 (`self.activated_val`) 따라서 backpropagation은 반드시 forward pass 이후에 해야한다.
다음 레이어의 gradient을 구하기 위해서 $\dfrac{\partial L}{\partial z_{31}}, \dfrac{\partial L}{\partial z_{32}}$가 필요하다. 이를 아래와 같이 구할 수 있다.
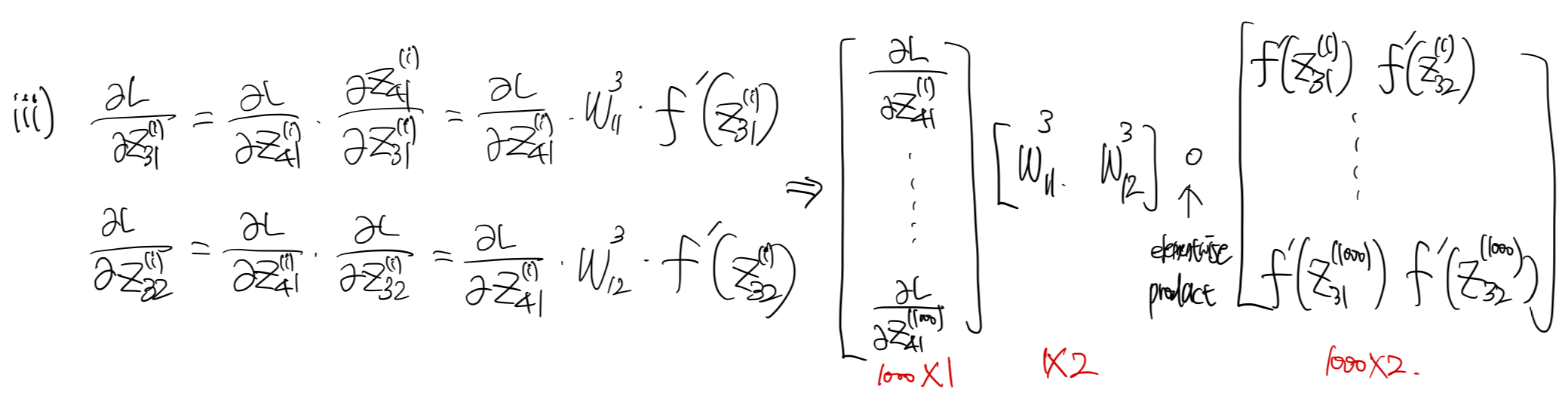
중간에 elementwise product 연산이 들어가있음에 주의해야한다.
다음으로 두번재 Linear 레이어에 대한 gradient을 구해보자.
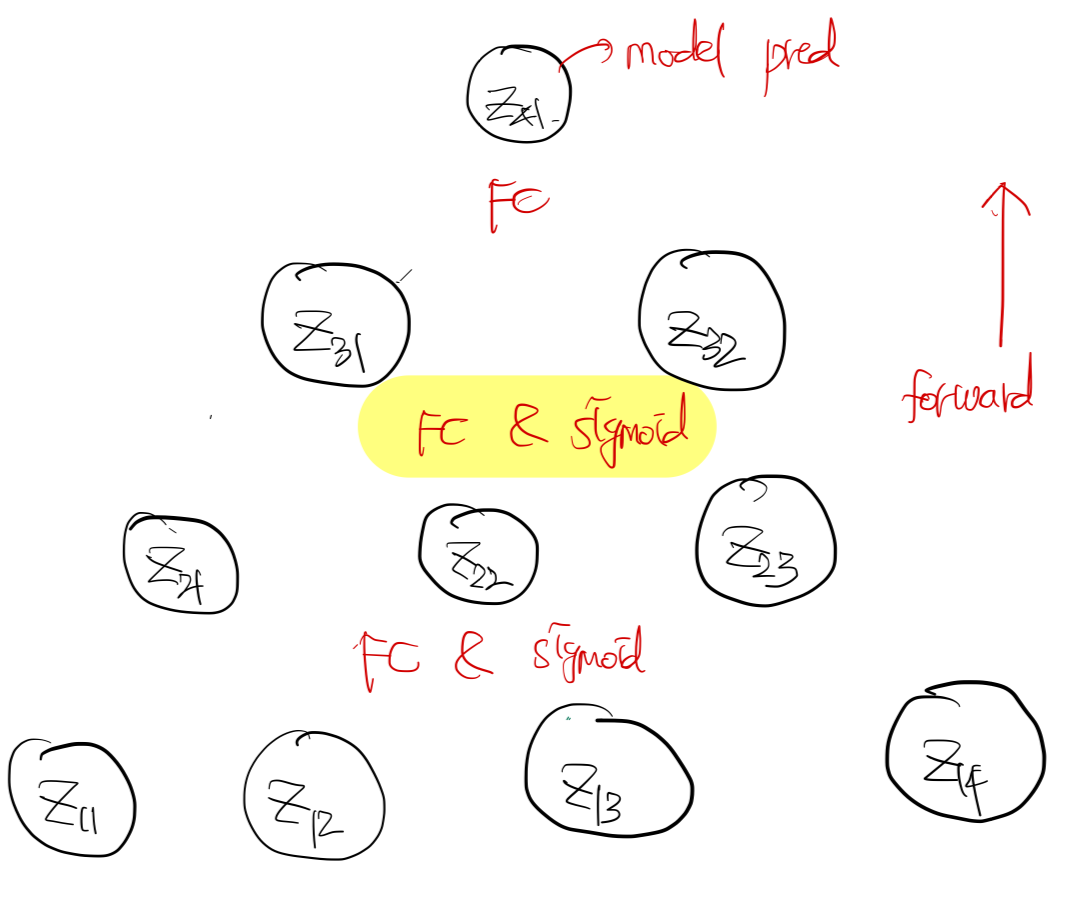
먼저, $z_{31}, z_{32}와 z_{21}, z_{22}, z_{23}$ 사이의 관계를 정의해보자.
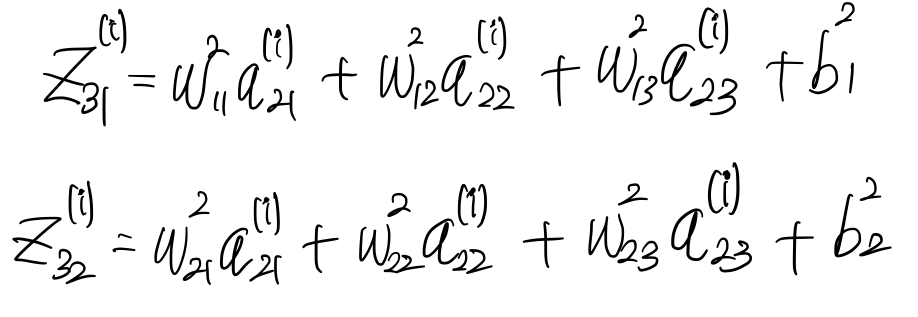
이전 단계에서 $\dfrac{\partial L}{\partial z^{(i)}_{31} }, \dfrac{\partial L}{\partial z^{(i)}_{32} }$을 구했다. 이를 사용하여 $\dfrac{\partial L}{\partial W^2}, \dfrac{\partial L}{\partial b^2}$을 구하면 아래와 같다.

또한 다음 스텝을 위해서 $\dfrac{\partial L}{\partial z^{(i)}_{21}}, \dfrac{\partial L}{\partial z^{(i)}_{22}}, \dfrac{\partial L}{\partial z^{(i)}_{23}}$을 구해두면 아래와 같다.
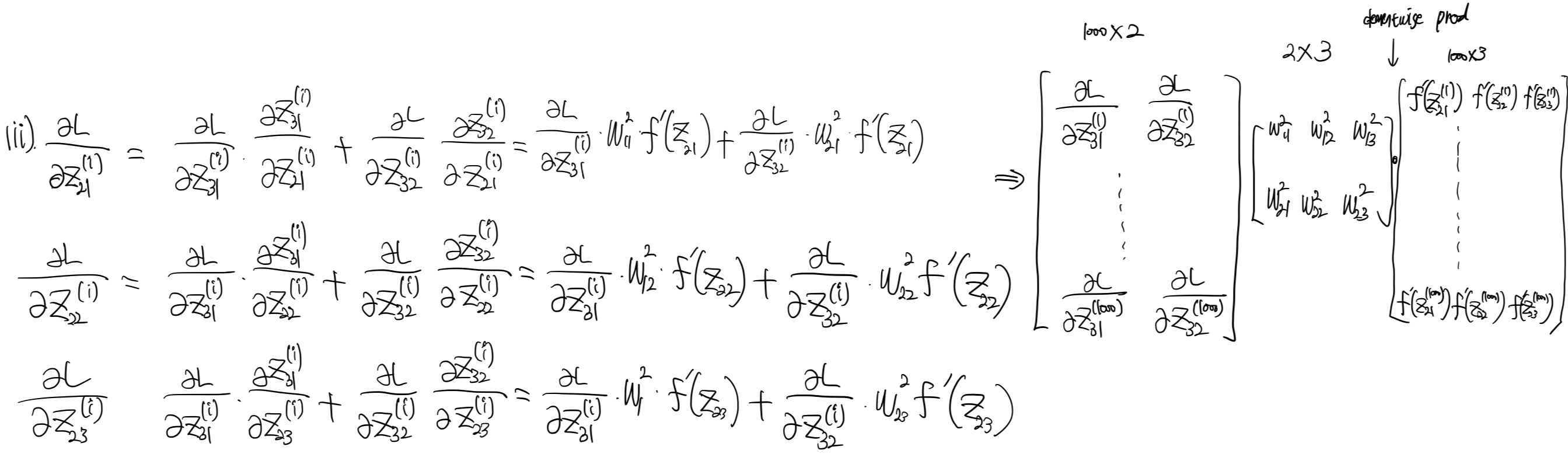
마지막으로 첫번재 레이어의 파라미터에 대한 gradient을 구해보자.
서두에서 언급했듯이, 첫번째 레이어의 입력값은 활성함수를 통과한 값이 아니기 때문에 weight matrix에 대한 gradient에서 활성함수를 곱하는게 아니라 기존의 입력값을 구하는 차이점이 있다. 이를 아래와 같이 정리할 수 있다.
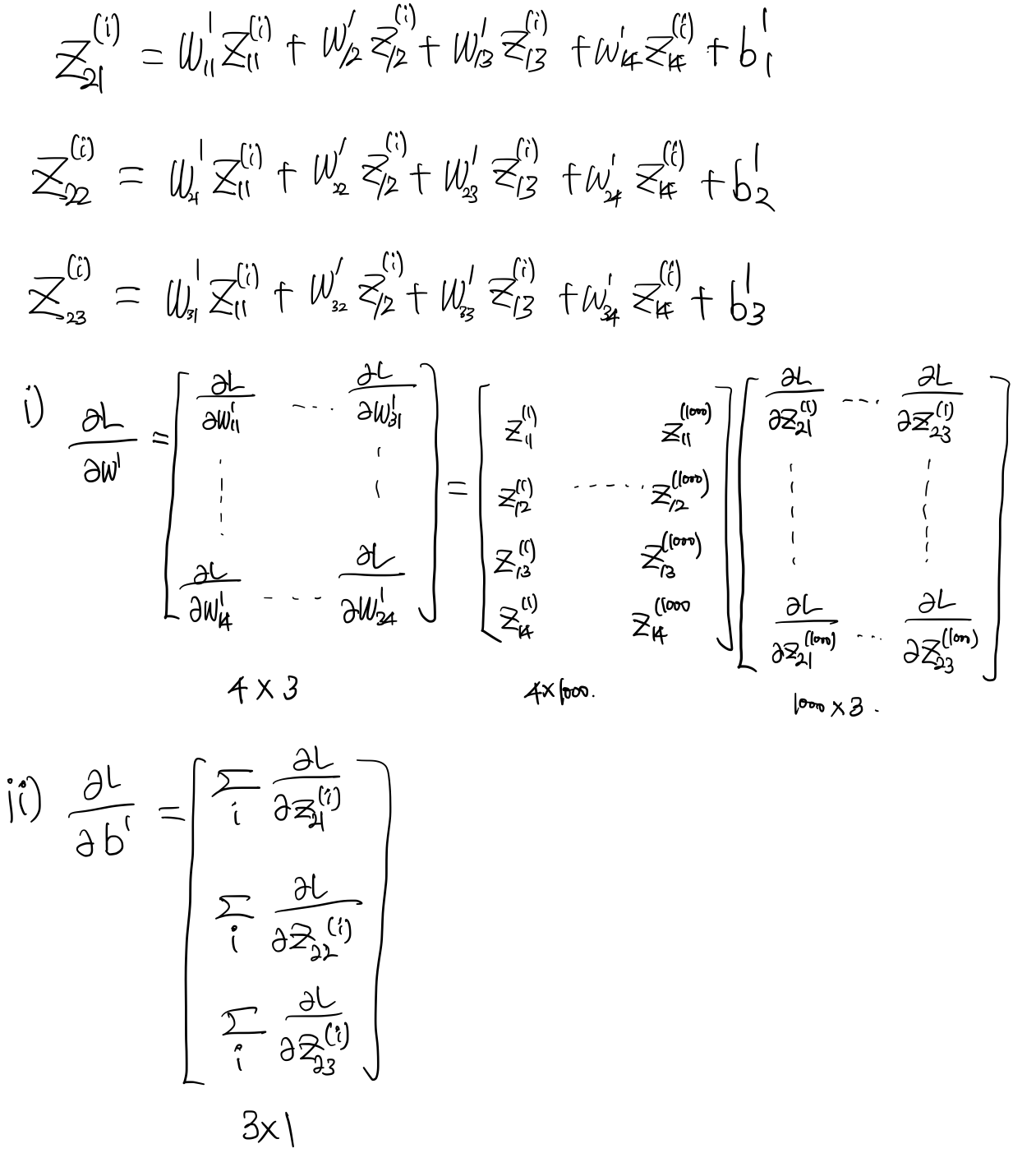
자, 이제 gradient을 모두 수학적으로 유도해봤다. 이제 코드를 다시 한번 살펴보자.
class NeuralNetwork(BaseNeuralNet):
...
def backward(self, y, pred, X):
step = 1
delta = (pred - y)
for layer in self.layers[::-1]:
if layer.__class__.__name__ != "Linear":
continue
activated = self.activated_val[-step]
layer.bias_grad = delta.sum(axis=0) # columnwise sum
layer.weight_grad = np.dot(activated.T, delta) # when initial layer, activated value is equal to input matrix, e.g., X
delta = np.dot(delta, layer.weight.T) * (activated) * (1 - activated)
step += 1
def step(self, lr):
for layer in self.layers:
if layer.__class__.__name__ == "Linear":
layer.weight -= lr * layer.weight_grad
layer.bias -= lr * layer.bias_grad
def zero_grad(self):
for layer in self.layers:
if layer.__class__.__name__ == "Linear":
layer.weight_grad = None
layer.bias_grad = None
- 가장 마지막 레이어의 prediction 값에 대한 gradient을 구한다. (`delta = pred-y`)
- 여기서 `self.activated_val`의 첫번째 값은 최초의 입력값을 그대로 넣었다. 따라서, `backward` 메써드의 `for loop`의 마지막 부분의 `activated` 값은 활섬함수를 통과한 값이 아니라 최초의 입력값이 나온다. 따라서, 첫번째 레이어에서도 weight에 대한 gradient을 올바르게 구할 수 있다.
- `step` 메써드는 `lr`만큼 파라미터를 이동시킨다. 현재는 나이브한 gradient descent로 구현되었다.
Experiment
이제 구성한 neural net의 파라미터를 데이터를 통해 학습시켜보자. 원래는 train/validation으로 나누고 validation에 대한 loss을 살펴봐야하는데, 이번 포스팅에서는 train loss을 살펴보고 validation loss는 다음에 구현하기로 한다. 아래와 같이 main script을 작성해보자.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
def train(epoch):
n = 1000
k = 4
struct = [4, 3, 2, 1]
X = np.random.randn(n, k)
y = np.cos(X).sum(axis=1).reshape(n,1)
nn = NeuralNetwork(struct=struct, n=n)
loss_ = []
for _ in range(epoch):
# forward pass
pred = nn.forward(X)
# calculate loss
loss = mean_squared_error(y, pred)
loss_.append(loss)
# backward
nn.backward(y, pred, X)
# gradient descent
nn.step(0.001)
# clear gradient
nn.zero_grad()
sns.lineplot(loss_)
plt.ylabel("loss")
plt.xlabel("iteration")
plt.show()
if __name__ == "__main__":
train(50000)
총 5만번의 epoch이며 batch gradient descent로 진행한다. 보통 deep learning에서 학습을 진행할 때는 mini-batch로 진행한다. 이 부분도 future work로 남겨둔다. train loss는 아래와 같다.
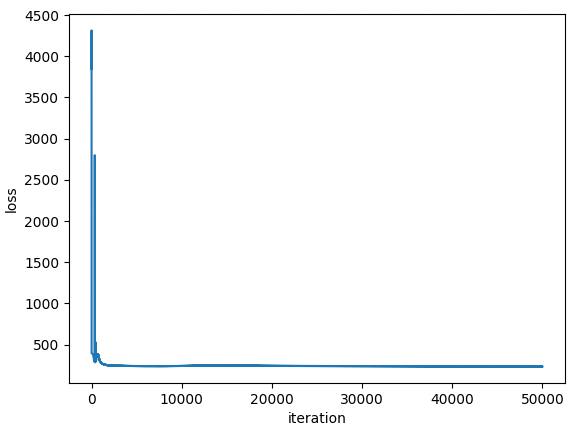
- train loss가 초반에 몇번 진동하는 것을 제외하면 iteration이 늘어남에 따라서 안정적으로 수렴한다.
- 현재는 dropout, batch normalization, xavier initalization 등이 구현되어 있지 않다. 만약 이런 테크닉을 추가한다면 초반의 진동하는 loss을 막을 수 있지 않을까 싶다.
Conclusion
MLP의 gradient을 직접 수학적으로 유도해보고 이를 pure numpy 코드로 구현해보았다. MLP를 numpy로 작성하다보니.. 다른 neural net (CNN, LSTM 등..)도 pure numpy로 구현해보고 싶은 욕심이 생겨서 아래의 repository을 파고 구조화하여 코드를 작성하고자 한다.
https://github.com/bohyunshin/deep-learning-with-pure-numpy
GitHub - bohyunshin/deep-learning-with-pure-numpy
Contribute to bohyunshin/deep-learning-with-pure-numpy development by creating an account on GitHub.
github.com
위에서 언급했듯이 mini-batch, batch normalization, xavier initalization 등 해야할 것이 산더미이다.. 근데 이렇게 직접 numpy로 구현하고 loss가 떨어지는 것까지 확인하니 pytorch을 사용하여 추상적으로 코딩하는 것보다 이해가 훨씬 잘 되는 것 같다. 앞으로도 시간 날 때마다 꾸준히 이 레포를 채워나가야겠다 :)
'ML&DL > Basics' 카테고리의 다른 글
| [ML / DL] Backpropagation in softmax function (1) | 2024.08.31 |
|---|---|
| [ML / DL] Cross entropy loss function in classification problem (12) | 2024.07.24 |
| [DL / Paper review] Auto-Encoding Variational Bayes (2) | 2023.05.06 |
| [DL] Why multiple layer perceptron? (0) | 2023.04.25 |
| [DL] Backpropagation (0) | 2023.03.20 |




댓글