- 논문 링크(1689회 인용)
Summary
- 유저에게 양질의 top-N 추천을 해주기 위해 error 기반 RMSE 지표가 아니라 accuracy 기반 recall&precision 지표를 제안한다.
- 또한 테스트 데이터 세트를 섬세하게 설계해야함을 보여준다.
- 매우 인기있는 아이템을 테스트 데이터에 포함한다면, 개인화된 추천을 하지 않는 알고리즘과 개인화 추천 알고리즘간의 성능 차이가 크게 나질 않아서 편향적으로 해석할 수 있다.
- 본 논문에서는 평점을 잘 맞추는 것이 중요한게 아니라 top-N 추천에 유저가 좋아하는 아이템을 포함시키는 것이 중요하다. 이런 측면에서 기존의 cf를 조금 변형한 알고리즘을 제안하고, 이것이 다른 알고리즘에 비해 우수한 성능을 보인다.
- normalize되지 않은 item-item based CF, 비어있는 값을 모두 0으로 채우고 SVD를 수행한 pure SVD
Motivation
- 기존의 cf 알고리즘은 RMSE을 줄이는 것이 주요한 목표였지만, RMSE가 작아진다고 해서 추천 품질이 꼭 좋아지는 것은 아니라는 연구 결과도 있었다.
- 실질적으로 유저에게 좋은 품질의 추천을 해주기 위해서는 그들에게 추천하는 n개의 아이템에 그들이 좋아하는 아이템이 포함되어야 하고, 더 상위로 포함될 수록 좋다.
- 본 논문은 이런 motivation을 가지고 RMSE을 줄이는데 목적이 아닌, top-N 추천에 유저가 좋아하는 아이템을 포함하는 것에 집중하여 논의를 진행한다.
Approach
Testing methodology
- 데이터를 훈련 데이터와 테스트 데이터로 나눈다. 다만, 테스트 데이터는 평점 5점 만점을 받은 데이터만 포함한다. 동일한 작업을 넷플릭스 데이터, movielens 데이터에 적용한다.
- 유저 $u$에 의해 매겨지지 않은 1000개의 아이템을 랜덤하게 추출한다. 유저 $u$는 이 1000개의 아이템 대부분을 좋아하지 않는다고 가정한다.
- 테스트 데이터 $i$와 1000개의 아이템에 대해 평점을 예측한다.
- 1001개의 아이템을 평점 순으로 나열한다. $p$를 테스트 아이템 $i$의 순위라고 하자. 가장 해피한 상황은 $p=1$로써, 다른 1000개의 아이템보다 제일 먼저 아이템 $i$가 추천되는 상황이다.
- 만약 $p \leq N$이라면 'hit' 되었다고 가정한다.
recall과 precision은 아래와 같이 정의된다.

Popular items vs long-tail
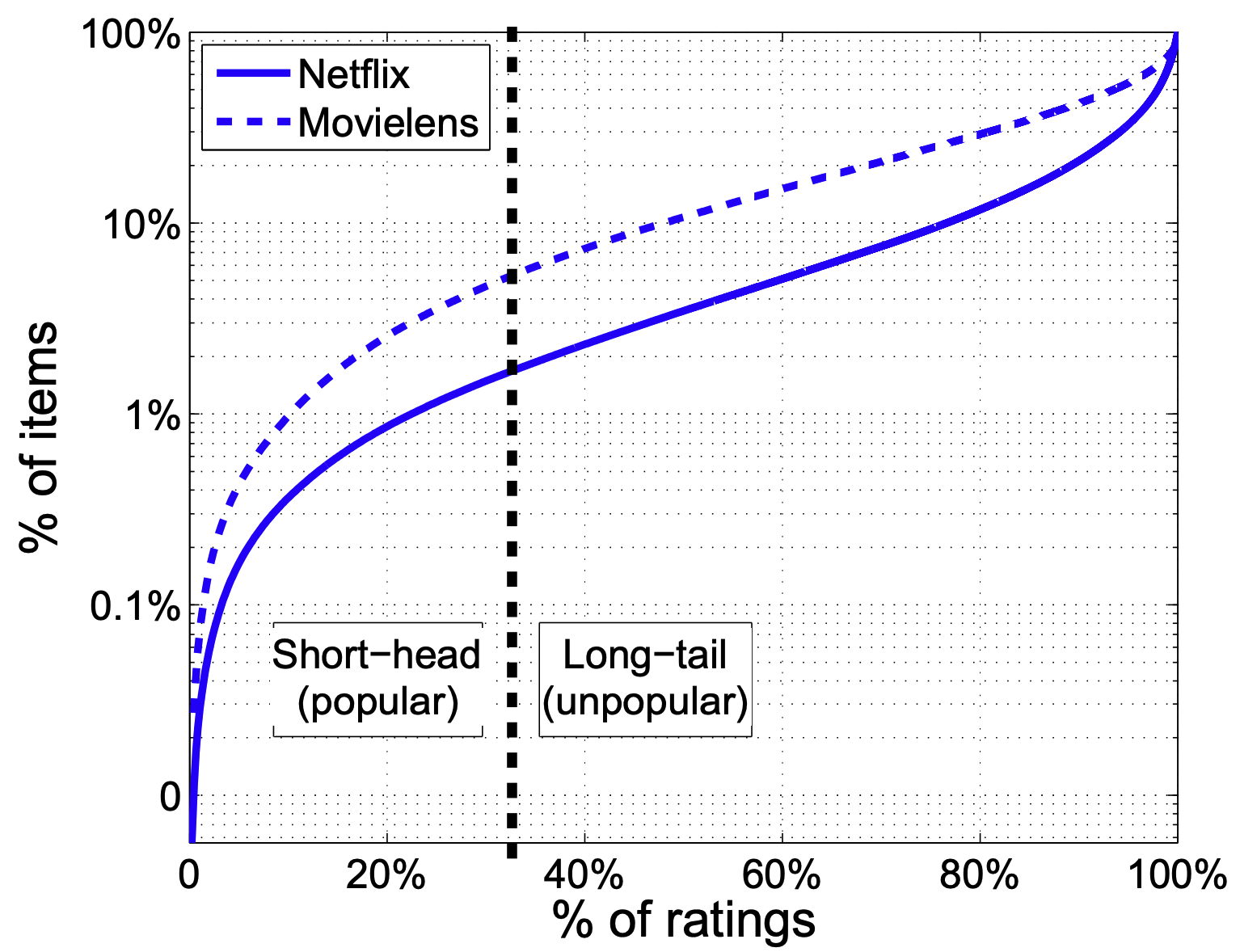
- 위 그림은 넷플릭스 데이터에서 33%의 평점이 1.7%의 아이템에 집중되어 있음을 보여준다. 즉, 다수의 평점이 매우 인기있는 아이템에 집중된 것이다. movielens 데이터도 크게 다르지 않은 상황을 보여준다.
- 매우 인기 있는 데이터를 short-head, 그 외의 데이터를 long-tail이라고 하자.
- 본 논문에서는 테스트 데이터에 short-head까지 포함한다면, 실험 결과가 편향됨을 보인다.
- 즉, 매우 인기있는 아이템에 대한 추천은 개인화되지 않은 알고리즘이든, 개인화된 알고리즘이든 동일하게 좋은 성능을 보여 잘못하면 개인화된 알고리즘을 쓸 필요가 없다고 해석될 수 있다는 것이다.
- 따라서, 테스트 데이터 세트를 구성할 때 short-head을 제외하는 것의 중요성을 강조한다.
Collaborative algorithms
- Non personalized models
- MovieAvg: 가장 높은 평점을 보이는 N개의 영화를 추천하는 방법
- TopPopular: 가장 많은 수의 평점을 보이는 N개의 영화를 추천하는 방법
- Neighborhood models
- correlation neighborhood: $\hat{r}_{ui} = b_{ui} + \dfrac{\sum_{j \in D^k(u;i)} d_{ij}(r_{ui} - b_{ui})}{\sum_{j \in D^k (u;i) } d_{ij}}$
- non-normalized cosine neighborhood: $\hat{r}_{ui} = b_{ui} + {\sum_{j \in D^k(u;i)} d_{ij}(r_{ui} - b_{ui})}$
- 평점을 예측하는 문제가 아니기 때문에 굳이 분모에 normalizing term을 둘 필요가 없다.
- 이웃하는 아이템이 많을 수록 더 큰 prediction 값을 가진다.
- Latent factor models
- SVD++
- AsySVD
- PureSVD
- 평점을 예측하는 문제가 아니기 때문에 결측치를 모두 0으로 채우고 conventional SVD을 진행한다.
- $\hat{\mathbf{R}} = \mathbf{U} \cdot \mathbf{\Sigma} \cdot \mathbf{Q}^T$
Results
넷플릭스 데이터에 대한 실험 결과만 정리한다.
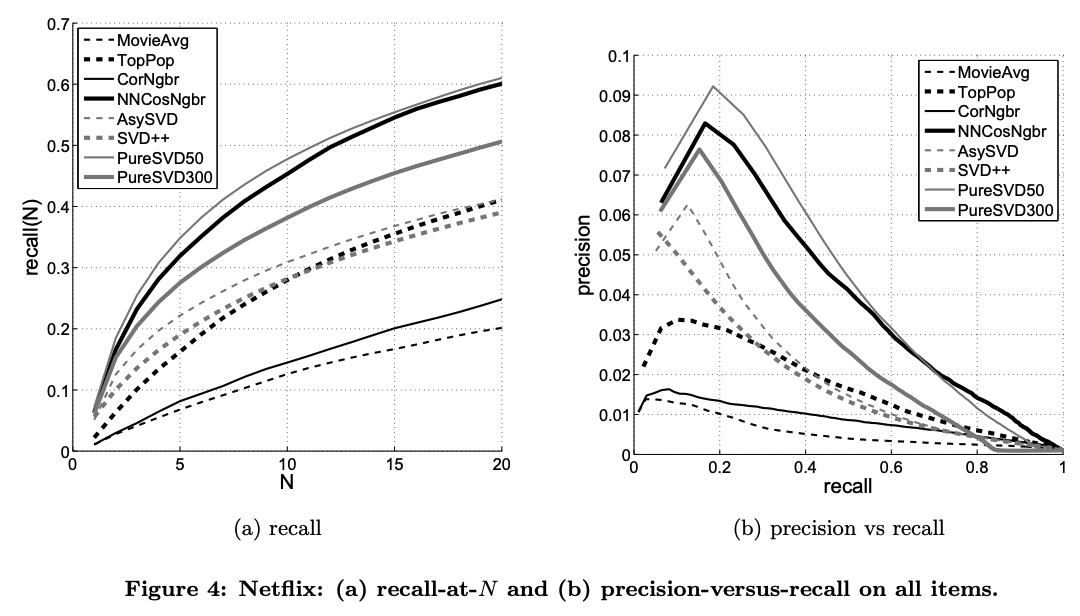
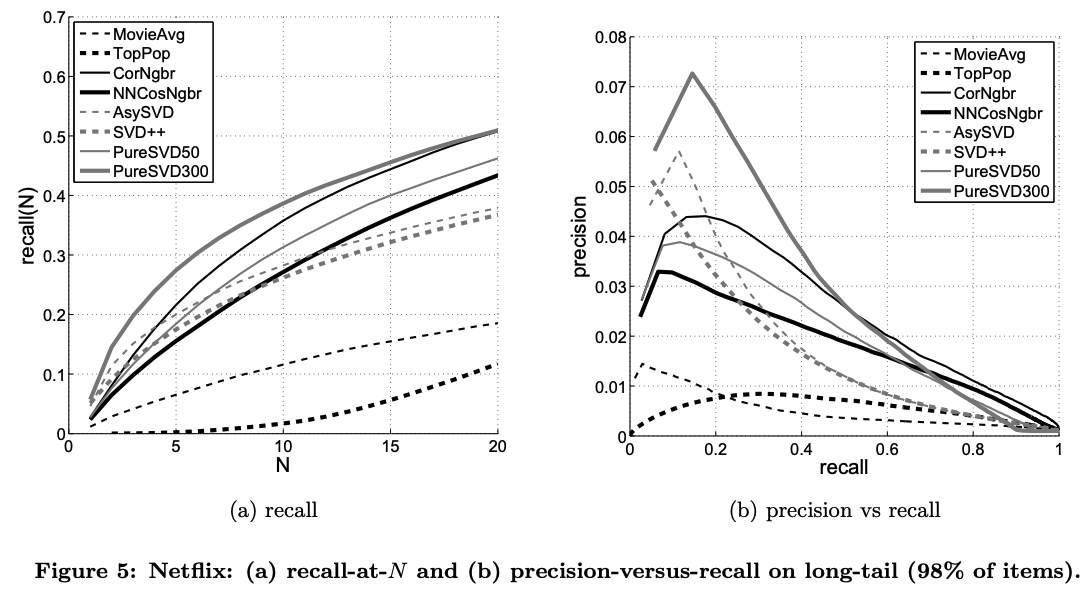
- 위 그림은 테스트 데이터에 short-head, long-tail을 모두 포함시킨 경우, 아래 그림은 테스트 데이터에 long-tail만 포함시킨 경우이다.
- 두 종류의 데이터를 모두 포함했을 경우 TopPop 방법이 AsySVD 등과 비슷한 성능을 보였다. 즉, 개인화되지 않은 추천이 개인화된 추천만큼의 성능을 낸다는 것이다.
- 아래 그림에서 long-tail만 포함했을 경우, 개인화되지 않은 추천인 MovieAvg와 TopPop은 훨씬 안 좋은 성능을 보였다.
- 두 경우의 데이터에 대해, pureSVD와 NNCosNgbr 방법이 모두 좋은 성능을 보였다.
Conclusion
- 추천 시스템 분야에서 알고리즘의 성능을 평가하는 지표로 RMSE뿐만 아니라 precision, recall도 고려해야함을 깨달았다.
- 또한 추천 시스템이라는 분야에서 대부분의 사람들이 좋아하는 아이템은 각별히 다뤄야함도 알게 되었다.
- 추천 시스템 분야에서 많이 논의되는 문제를 알아야 알고리즘을 더 전략적으로 세울 수 있을 것 같다는 생각이 들었다.




댓글