- 논문 링크(1212회 인용)
Summary
- 유저x아이템 행렬은 대부분의 값이 결측치인 sparse 행렬이다. 결측치를 유저의 부정적인 반응으로 보는 방향과 아예 unknown 값으로 취급하는 방향이 있다.
- 본 논문에서는 이 두 양극단의 중간점으로 두 가지 방법을 제시한다.
- 하나는 행렬의 결측치 값에 가중치를 주는 것이다. 여기서 0 또는 1이라면 앞서 말한 두 방향이겠지만, 0과 1 사이의 값을 줌으로써 결측치도 살리고 좀 더 현실적인 가정을 모형에 포함한다.
- 다른 하나는 positive feedback은 모두 포함하되, 결측치를 랜덤하게 추출함으로써 모델을 구성하고 나중에 합치는 방향이다.
- weighted low rank approximation: negative examples에 부여하는 weight에 따라 중요도를 다르게 설정하는 방법
- negative example sampling: 한번에 모든 negative example을 사용하는 것이 아니라, 샘플링하여 prediction을 구성한 다음, 최종 단계에서 ensemble하여 합치는 방법
Motivation
- 추천 시스템 분야는 유저x아이템 행렬에서 비어있는 값을 예측하는 문제를 풀고자 하는데 문제는 매우 많은 값들이 비어있다는 것이다.
- 전통적인 cf 알고리즘은 이 값들을 모두 유저의 부정적인 반응으로 간주하는데, 이는 아래의 문제점이 있다.
- 어떤 유저의 아이템 a에 대한 평점이 비어있다면, 이것이 아이템 a를 좋아하는데 이를 못보고 지나친 것인지, 아니면 정말로 아이템 a를 싫어하는지 확실하게 알 수가 없다.
- 따라서 결측치를 모두 유저가 부정적이라고 표현한 데이터로 간주한다면, 모델 결과가 biased 될 수 있다.
- 또는 결측치를 라벨링하는 방법도 있는데 이는 비용이 너무 많이 들고 잘못하면 유저들의 이탈을 초래할 수 있다.
- 이런 문제를 해결하기 위해, 본 논문에서는 결측치를 얼마만큼의 비율을 사용하여 negative examples로 다룰지 고민한다.
Approach
유저의 positive example만을 사용하는 cf를 one-class collaborative filtering (OCCF)라고 하자. 기존의 cf가 행렬에서 결측치인 값들을 negative example로 간주하여 사용했다면, OCCF는 이들이 negative example라고 생각하지 않는다.
Notation
- AMAN: All Missing As Negative
- AMAU: All Missing As Unknown
- $m$명의 유저, $n$개의 아이템
- $\mathbf{R} \in \mathcal{R}^{m \times n}$: positive example이라면 1, 결측치라면 0의 값을 가지는 유저x아이템 행렬
Problem Definition
$\mathbf{R}$에 근거하여 비어있는 positive examples을 찾는 것이 목표이다. 이를 One-Class Collaborative Filtering (OOCF)라 하자.
weighted low-rank approximation: wALS for OCCF
- $\mathbf{R} = (R_{ij})_{m \times n} \in \{ 0, 1 \}^{m \times n}$
- $\mathbf{W} = (W_{ij})_{m \times n} \in \mathcal{R}^{m \times n}_{+}$
- $\mathbf{X} = (X_{ij})_{m \times n}$: weighted low-rank approximation
weighted low-rank approximation은 low rank matrix인 $\mathbf{X}$을 아래 목적식을 통해 찾는 것이 목적이다.

- 관측된 $(i,j)$쌍에 대해서만 파라미터를 업데이트하는 것이 아니라 모든 쌍에 대해서 업데이트 한다.
- $(R_{ij} - X_{ij})^2$은 low-rank approximation에서 흔히 볼 수 있는 square error term이다.
- 단, 여기에 서로 다른 가중치인 $W_{ij}$가 곱해진다.
- $R_{ij} = 1$이면 $W_{ij} = 1$이다.
- $R_{ij} = 0$이면 $W_{ij} \in [0,1]$이다.
$\mathbf{X}$을 두 행렬로 분해하여 위 식을 다시 써보면 아래와 같다.
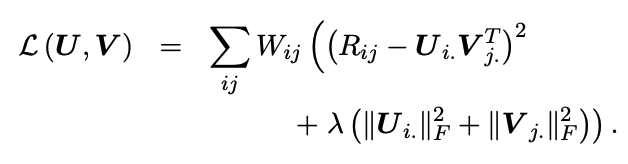
- $\mathbf{X} = \mathbf{UV}^T$
- $X_{ij} = \mathbf{U}_{i.} \mathbf{V}_{.j}^T$
- 파라미터에 대해 frobenius norm을 추가하여 과적합을 방지한다.
$\mathcal{L}(\mathbf{U}, \mathbf{V})$은 두 파라미터에 대한 함수이고 한 파라미터를 고정시킨채로 다른 파라미터를 차례로 업데이트하는 alternating least squares을 사용한다. 알고리즘은 아래와 같다.

$\mathbf{U}_{i.}, \mathbf{V}_{.j}$에 대한 closed form은 아래와 같다.
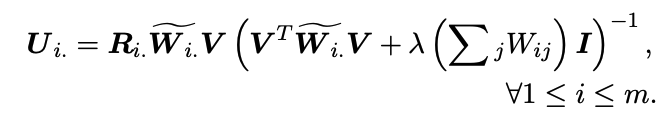

Weighting Schemes: uniform, user oriented and item oriented

- uniform scheme: 모든 유저와 아이템에 대해 negative example이 나타날 확률을 동일하게 가정한다.
- user-oriented scheme: 유저가 많은 positive examples을 가지고 있다면, 다른 아이템을 좋아하지 않을 가능성이 크다고 가정한다. 즉, positive examples의 아이템 수에 비례하여 negative examples의 확률을 정한다.
- item-oriented scheme: positive example이 적은 아이템은, 이 아이템이 결측치일 때 negative example일 확률이 크다고 가정한다. 다수의 유저에게 선택받지 못한 아이템은 다른 유저에게도 선택받지 못할 가능성이 크다는 가정이다.
Sampling-based ALS for OCCF
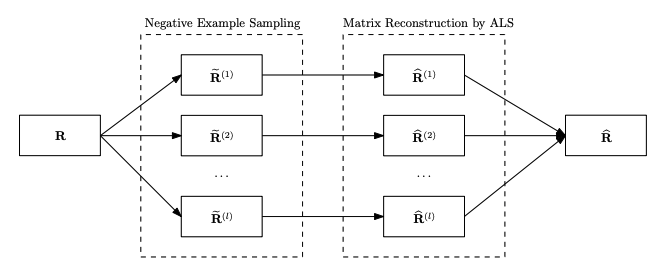
- Phase 1: $\mathbf{R}$에 있는 positive example은 모두 포함한 채로 가정한 확률 분포에 의해서 negative example을 샘플링하여 $\tilde{\mathbf{R}}^{(i)}$을 만든다.
- $\tilde{\mathbf{R}}^{(i)}$을 사용하여 wALS을 통해 $\hat{\mathbf{R}}^{(i)}$을 만든다.
- $\hat{\mathbf{R}}^{(i)}$을 합쳐서 최종 추정값 $\hat{\mathbf{R}}$을 만든다.
Sampling Scheme
- $\tilde{\mathbf{R}}^{(i)}$을 만들기 위해 가정하는 확률분포 $\hat{\mathbf{P}}$을 제시한다.
- uniform random sampling: $\hat{P}_{ij} \propto 1$
- user-oriented sampling: $\hat{P}_{ij} \propto \sum_i I[R_{ij} = 1]$
- 어떤 유저가 아이템을 더 많이 봤으면, 그 유저가 보지 않은 다른 아이템은 negative example일 확률이 높다고 가정한다.
- item-oriented sampling: $\hat{P}_{ij} \propto 1/ \sum_j I[R_{ij} = 1]$
- 어떤 아이템이 다른 유저에 의해 덜 봐졌다면, 그 아이템을 보지 않은 유저도 추후에 보지 않을 확률이 높다고 가정한다.
Results
Metric
Mean Average Precision
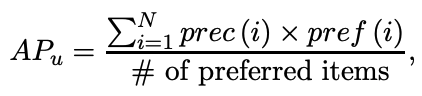
Half-life utility

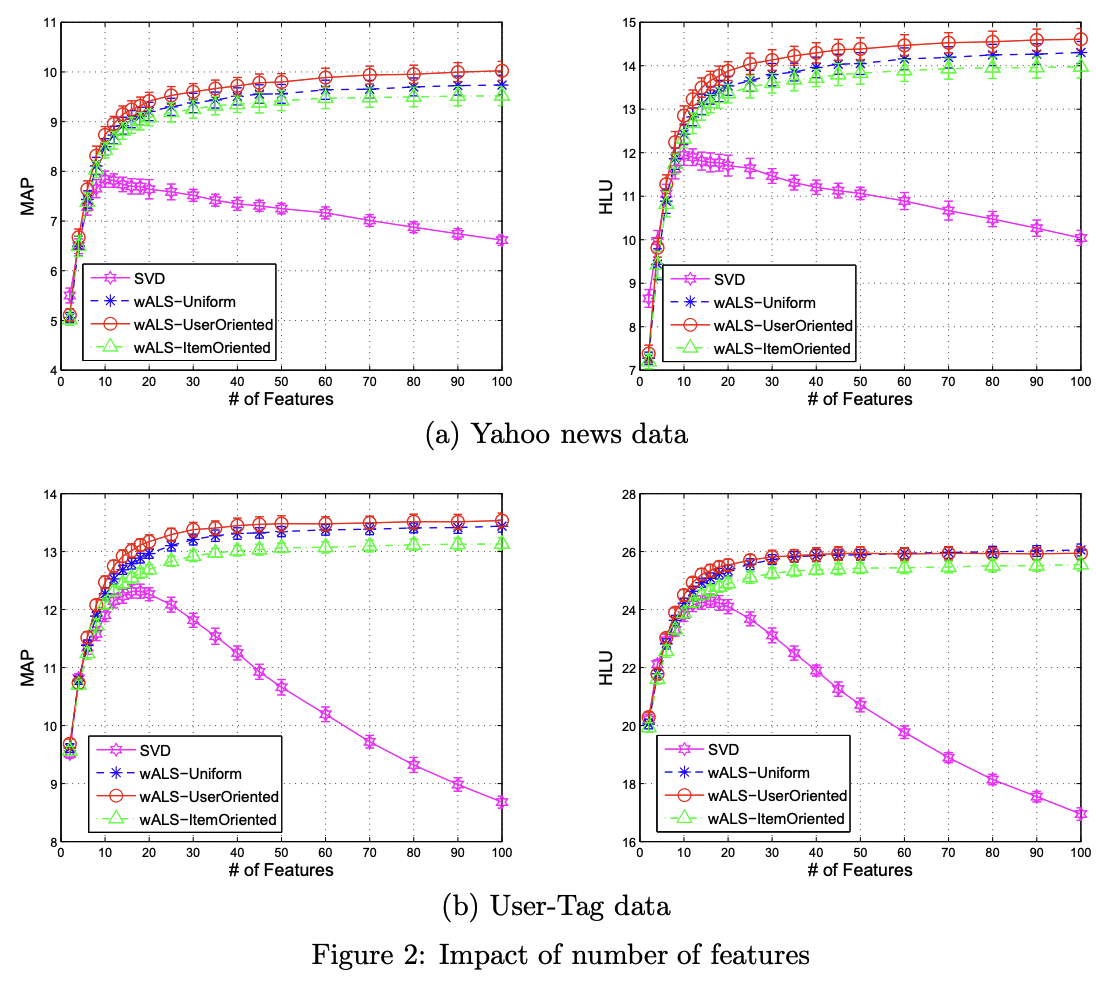
- SVD는 latent feature의 수가 늘어나자 평가지표에서 불안전한 모습을 보였다.
- 논문에서 제안한 방법은 안정적인 수렴을 보였다.
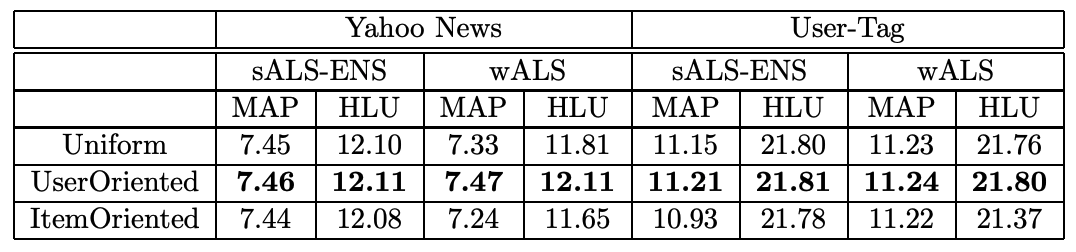
- user-oriented 방법이 제일 좋은 결과를 보여줬고 uniform은 그 중간쯤의 결과를 보여줬다.
Conclusion
- 본 논문에서는 sparse한 유저x아이템 행렬에서 결측치를 어떻게 활용할 것인지, 일종의 방향을 제시해주었다.
- 기본적으로 이 결측치를 모두 negative example라고 일괄적으로 보면 안 되며 이를 가중치를 통해 조정하는 것이 핵심 아이디어이다.
- 여태까지 공부한바로는 explicit feedback을 이용한 모델은 관측된 데이터에 대해서만, implicit feedback을 이용한 모델은 모든 데이터에 대해서 최적화를 진행한다. 본 논문은 모든 데이터를 이용할 때, 주의해야할 점을 짚어줬다는 측면에서 의의가 있지 않을까 싶다.



댓글