서울대학교 딥러닝 기초 강의를 듣고 정리하였다.
회귀 문제든, 분류 문제든, stochastic gradient descent의 일반적인 식을 공통적으로 도출할 수 있다. 이번 포스팅에서는 이 식을 유도해보면서 어떤 공통점을 찾을 수 있는지 알아본다.
통계학을 전공하다보면, 수리통계학 과목을 필수적으로 수강해야하고 여기에서 나오는 단골손님이 exponential family이다.
확률분포 $p(y | x ; \theta)$의 exponential family 형태는 아래와 같다.
\[ p(y ; \eta) = b(y) exp(\eta^T T(y) - a(\eta)) \]
- $\eta$: natural parameter
- $T(y)$: sufficient statistics for $p(y | x ; \theta)$
- $a(\eta)$: log partition function
베르누이 분포를 예시로 살펴보자.

그러면 멀쩡한 확률분포를 왜 굳이 이렇게 exponential family 형태로 바꾸는 것일까?
개인적인 생각으로는, 정규분포, 포아송분포, 베르누이 분포 등 다양한 확률 분포를 하나의 일반적인 형태로 나타낼 수 있다는 장점이 가장 크다고 생각된다. 또한, 이 일반적인 형태에서 충분통계량 (sufficient statistics)도 자동으로 유도되기 때문에 이를 사용하기에 편리하다.
이정도로 알고 있었는데, 교수님의 강의를 통해서 exponential family의 또 다른 용도를 알게 되었다. 그것은, generalized linear models의 gradient descent 공식을 유도할 때 exponential family가 쓰인다는 것이다.
generalized linear models이란 무엇인가? 회귀 문제에서는 출력값 $y$가 연속형 변수이다. 분류 문제에서는 출력값 $y$가 0과 1의 값을 가지지만, 사실상 $(0,1)$의 구간값을 가지는 확률을 모델링한다. 만약, 정수형 변수를 가지는 출력값을 가지고 싶다면? 이는 또 다른 문제이다. 이와 같이 연속형 변수뿐만 아니라 $(0,1)$의 범위를 가지는 변수, 정수형 변수를 모델링하는데 사용되는 모형을 통틀어서 generalized linear models이라 한다.
GLM은 기본적으로 확률분포 $p(y | x ; \theta)$가 exponential family을 따른다고 가정한 상태에서, 아래 함수를 찾는 것을 목표로 한다.
\[ h(x) = E[T(y) | x] \]
오른쪽 항을 자세히 살펴보자. sufficient statistics을 $T(y) = y$로 두고 생각해보자. 모든 $x$가 주어진 상태에서 $y$의 기대값이다. ML이든 DL이든 입력값 $x$을 넣었을 때, 가능한 출력값을 얻는 것이 목표이다. 그런데 입력값은 유한개가 아니다. 따라서 모든 가능한 입력값에 대해서 나오는 출력값의 대표값을 뽑는 것이다. 통계학에서 대표값으로써 많이 쓰이는 것이 기댓값이다. 따라서 $h(x)$는, 가능한 모든 $x$에 대해서 나오는 출력값의 대표값이라고 해석할 수 있다.
여기서 $h(x)$는 일종의 hypothesis이다. $x,y$가 어떤 관계를 맺고 있을 것이라는, 가정이다. 그 관계는 identity일 수도 있고, logit일 수도 있고 다양하다. 관계가 선형이든, 비선형이든, gradient descent을 통해 그 함수를 근사시켜서 구하는 것이 최종 목적이다.
또한 generalized linear models이다. 무슨 말이냐면, 모델 어딘가에는 선형 관계가 들어간다는 것이다. 이는 GLM이 exponential family의 natural parameters을 선형($\eta = \theta^T x$)으로 가정하는 부분을 반영하는 것이다.
이전 포스팅에서 cost function을 최소화하는 것은 likelihood function을 최대화하는 것과 동일함을 보였다. 이를 다시 생각해보면, cost function을 최소화할 때 사용하는 gradient와 likelihood function을 최대화할 때 사용하는 gradient을 서로 교환해서 사용할 수 있다는 뜻이다. 이 사실을 이용하여 likelihood function의 gradient을 구하여 cost function에 대한 stochastic gradient descent의 식을 유도해보자.
likelihood function을 최대화하기 위한 gradient은 아래와 같다.

여기서, likelihood function은 최대화 문제이고 cost function은 최소화 문제 이므로 -1을 곱해 부호만 바꿔주면 된다. 식을 전개할 때 1번에서는 아래의 사실이 사용됐다.
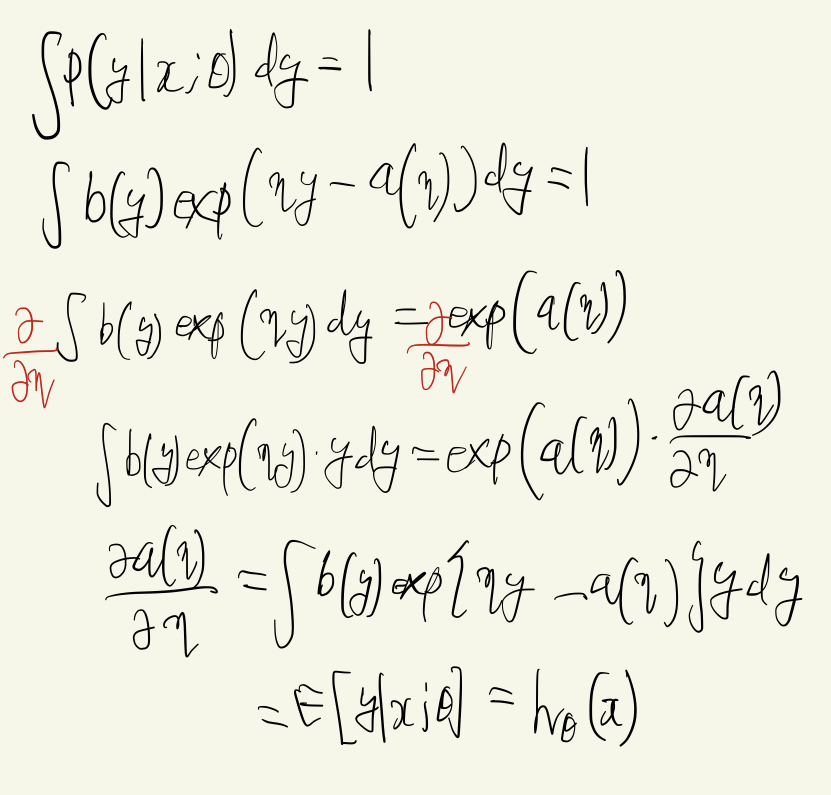
최종적으로 아래와 같이 도출된다.

놀라운 사실은, 확률분포 $p$에 대해 특별한 가정을 하지 않았다는 것이다. 즉, 회귀문제이든, 분류문제이든, gradient descent의 형태는 위와 같은 식으로 동일하게 정리된다.
교수님께서 강의를 하시며, 위와 같이 gradient descent의 형태가 동일하게 정리된다는 사실이 중요함을 거듭 강조하셨다. 이 사실이 나중에 어떤 식으로든 쓰이리라.. 믿으며 포스팅을 마쳐본다.
'ML&DL > Basics' 카테고리의 다른 글
| [DL / Paper review] Auto-Encoding Variational Bayes (2) | 2023.05.06 |
|---|---|
| [DL] Why multiple layer perceptron? (0) | 2023.04.25 |
| [DL] Backpropagation (0) | 2023.03.20 |
| [ML / DL] Cost function과 Maximum likelihood estimation과의 관계 (0) | 2023.03.19 |
| [DL] Batch / Stochastic / Mini batch Gradient Descent (0) | 2023.03.19 |




댓글