Motivation
segment tree 자료구조는 아래의 문제를 해결하는데 사용된다.
1. 1차원 배열의 i번째 수부터 j번째 수까지의 연속 합을 구해야할 때 (총 $m$번)
2. 배열의 i번째 수가 변경되는 쿼리를 같이 처리해야할 때 (총 $k$번)
1번의 문제만 해결해야한다면, 부분 합 (Prefix Sum) 문제로 치환하여, $O(n+m)$의 시간 복잡도로 해결할 수 있다.
하지만, 2번의 문제까지 추가가 된다면 상황이 복잡해진다.
부분 합을 이미 구해 놓은 상태에서, i번째 수가 변경된다면 부분 합을 다시 업데이트해야한다. 즉, $k$번만큼 배열의 수가 변경될때마다 부분 합을 업데이트해야하므로 여기서 $O(nk)$의 시간 복잡도가 발생한다. 여기에 m개의 연속 합을 구해야하므로 최종 시간 복잡도는 $O(nk+m)$이다. $n,k,m$의 크기가 클 경우에는, 시간이 오래걸리므로 효율적인 알고리즘이 필요하고 여기서는 segment tree을 이용해서 $O((k+m)logn)$의 시간 복잡도로 문제를 해결해 보겠다.
Segment Tree
우선, segment tree의 이름을 쪼개서 생각해보자.
- segment: 배열을 연속하는 segment로 나누어 node로 지정하고 해당 node는 연속하는 segment의 합을 가지도록 한다.
- tree: 자료구조로 (완전)이진트리를 사용한다.
트리 자료구조를 사용하기 때문에, 부분합을 구할 때나 수를 변경하는 쿼리를 처리할 때나 $O(logn)$의 시간복잡도가 발생하는 것이다.
$[2,1,3,7,5,9,4,8,1]$의 값을 가지는, 길이가 9인 배열에서 segment tree을 사용해 변경이 발생하는 부분합 문제를 해결하는 과정을 살펴본다.
1. 트리 자료 구조 만들기
먼저, 트리 자료 구조를 아래 그림과 같이 만들어야 한다.

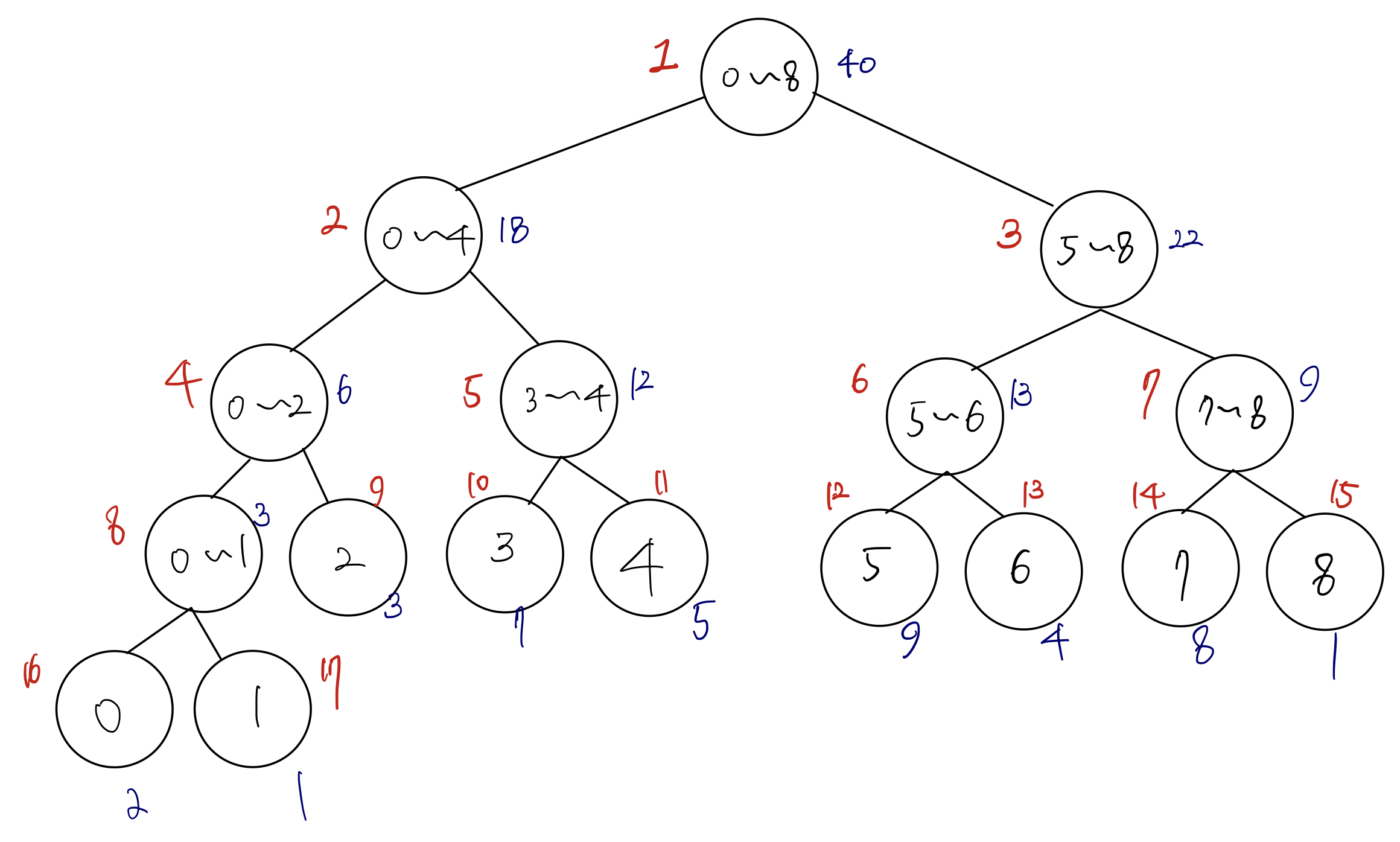
- 동그라미 안에 있는 수는 인덱스를 의미한다. 즉, 0~8의 의미는, 해당 노드가 0번째에서 8번째까지의 연속된 수들의 합의 값을 가진다는 뜻이다.
- 빨간색 숫자는 노드의 번호를 의미한다. 이진 트리이기 때문에, 왼쪽 자식 노드는 부모 노드 번호의 2배, 오른쪽 자식 노드는 부모 노드 번호의 2배 + 1이다.
- 노드 수만큼의 길이를 가지는
tree배열을 선언한다.- 길이가 n인 배열에서 위와 같은 이진 트리를 만들면, 그 높이는 $log_2 n$이다.
- $n$이 2의 거듭제곱이 아닐 경우를 대비해서 높이는 $h = ceil( log_2 n)$으로 구한다.
- 완전 이진 트리를 가정하면 노드의 개수는 $2^{h+1} - 1$이다.
- 완전 이진 트리가 아니라도, 같은 높이라면 이진 트리의 노드 개수가 더 적으므로 완전 이진 트리의 노드 개수만큼
tree배열을 선언한다.
tree배열의 i번째 원소 값을, i번째 노드가 가지는 해당 segment의 연속된 부분합으로 정의한다.- 재귀를 통해 segment를 시작하는 인덱스와 끝나는 인덱스가 같을 때까지 들어가고, 같다면 배열의 해당 인덱스 값을 반환한다.
- 왼쪽 자식 노드와 오른쪽 자식 노드의 값을 재귀적으로 구하여 부모 노드의 값을 구한다.
# n은 배열의 크기
# l은 해당 배열
l = [2,1,3,7,5,9,4,8,1]
tree = [0]*(2**(h+1))
def init(node, start, end):
if start == end:
tree[node] = l[start]
return tree[node]
tree[node] = init(node*2, start, (start+end)//2) + init(node*2 + 1, (start+end)//2 + 1, end)
return tree[node]
init(1, 0, n-1)위 코드를 실행하면, 각 노드에 아래와 같은 값이 저장된다.
2. 부분 합 구하는 함수 만들기
인자로 들어가는 것은 총 4가지이다.
start: 해당 노드가 시작하는 인덱스end: 해당 노드가 끝나는 인덱스left: 부분합을 구하고자 하는 segment의 시작하는 인덱스right: 부분합을 구하고자 하는 segment의 끝나는 인덱스
총 네 가지 상황이 발생할 수 있다.
- 노드 세그먼트의 인덱스 범위와 부분합 세그먼트의 인덱스 범위가 아예 맞지 않을 때: 0의 값을 반환한다.

- 노드 세그먼트의 인덱스 범위가 부분합 세그먼트의 인덱스 범위에 완전히 포함될 때: 해당 노드의 부분 합을 반환한다.

- 노드 세그먼트의 인덱스 범위가 부분합 세그먼트의 인덱스 범위를 포함할 때: 2번 케이스에 갈때까지 재귀를 수행한다.
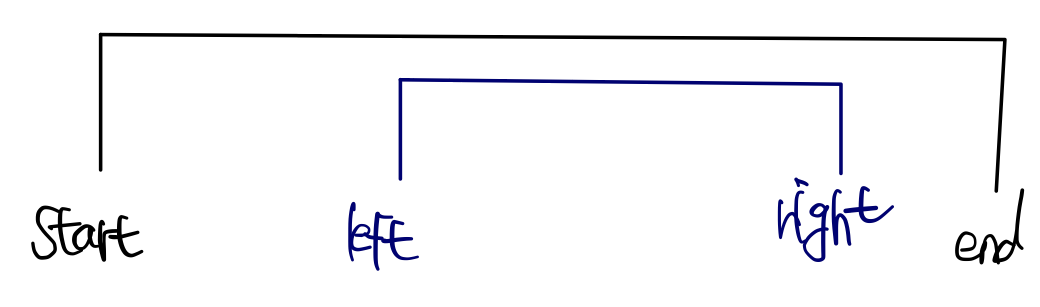
- 노드 세그먼트의 인덱스 범위와 부분합 세그먼트의 인덱스 범위가 일부 겹칠 때: 2번 케이스에 갈때까지 재귀를 수행한다.

이를 프로그램으로 옮기면 아래와 같다.
def subsum(node, start, end, left, right):
# case 2
if left <= start and end <= right:
return tree[node]
# case 1
if end < left or right < start:
return 0
# case 3 & 4
return subsum(node*2, start, (start+end)//2, left, right) + subsum(node*2 + 1, (start+end)//2 + 1, end, left, right)3. 업데이트하는 쿼리 만들기
- 바꾸고자 하는 인덱스의 기존 값과 새로운 값을
diff로 저장한다. - 해당 노드가 인덱스를 포함한다면, 해당 노드의 값에
diff만큼 더한다. - 해당 노드가 leaf node가 아닐 때까지 위 과정을 반복한다.
def update(node, start, end, index, diff):
if not (start <= index <= end):
return
tree[node] += diff
if start != end:
update(node*2, start, (start+end)//2, index, diff)
update(node*2 + 1, (start+end)//2 + 1, end, index, diff)BOJ 문제
https://www.acmicpc.net/problem/2042

전체 소스코드는 아래와 같다.
from math import log2, ceil
import sys
input = sys.stdin.readline
def init(node, start, end):
if start == end:
tree[node] = l[start]
return tree[node]
tree[node] = init(node*2, start, (start+end)//2) + init(node*2 + 1, (start+end)//2 + 1, end)
return tree[node]
def subsum(node, start, end, left, right):
if left <= start and end <= right:
return tree[node]
if end < left or right < start:
return 0
return subsum(node*2, start, (start+end)//2, left, right) + subsum(node*2 + 1, (start+end)//2 + 1, end, left, right)
def update(node, start, end, index, diff):
if not (start <= index <= end):
return
tree[node] += diff
if start != end:
update(node*2, start, (start+end)//2, index, diff)
update(node*2 + 1, (start+end)//2 + 1, end, index, diff)
n,m,k = map(int,input().split())
h = int(ceil(log2(n)))
tree = [0]*(2**(h+1))
l = []
for _ in range(n):
l.append(int(input()))
init(1, 0, n-1)
for _ in range(m+k):
a,b,c = map(int,input().split())
if a == 1:
b -= 1
diff = c-l[b]
l[b] = c
update(1, 0, n-1, b, diff)
if a == 2:
b -= 1
c -= 1
print(subsum(1, 0, n-1, b, c))
댓글