[BF] 16937번 두 스티커

https://www.acmicpc.net/problem/16937

알고리즘

• Brute Force
• Greedy (?)

풀이

포인트

• 주어진 n개의 스티커 중 두 개의 스티커만 사용하여 최대 넓이를 구한다는 점
• 스티커를 회전할 수 있고 스티커끼리 접할 수 있다는 점

Brute Force

전형적인 brute force 문제이다. n개의 스티커 중 2개를 골라서 스티커를 붙여보면서 최대 넓이를 가지는 스티커 조합을 찾으면 된다. 여기서 고민되는 부분이 스티커를 붙이는 것을 어떻게 구현하는지였다. 가장 먼저 생각난 점은, $h \times w$ 넓이에 한칸 한칸 for문을 돌면서 스티커를 붙여보는 것이었다. 그런데 이렇게 하면, 스티커를 붙일 수 있는 격자판과 스티커 최대 넓이가 100이므로 시간 복잡도가 꽤 커질 것 같았다.

따라서 주어진 n개의 스티커 중 2개의 스티커를 고르는 로직은 그대로 적용하되 스티커를 최대로 붙이는 과정을 아래와 같이 생각했다. 높이 10, 너비 9인 격자판에 스티커를 붙이는 상황을 생각해보자. 붙여진 스티커의 넓이를 최대로 하기 위해 $7 \times 5$ 스티커를 어디에 붙이는 것이 최선일까?
얼핏 보기에는, 다음 스티커가 주어지지 않았으므로 $10 \times 9$ 격자판에 $7 \times 5$를 모두 놓음으로써 탐색해야한다고 생각할 수 있다. 하지만 최대 넓이를 가지도록 하려면, $7 \times 5$ 스티커를 아래 그림과 같이 구석에다가 두는 것이 좋을 것이다.

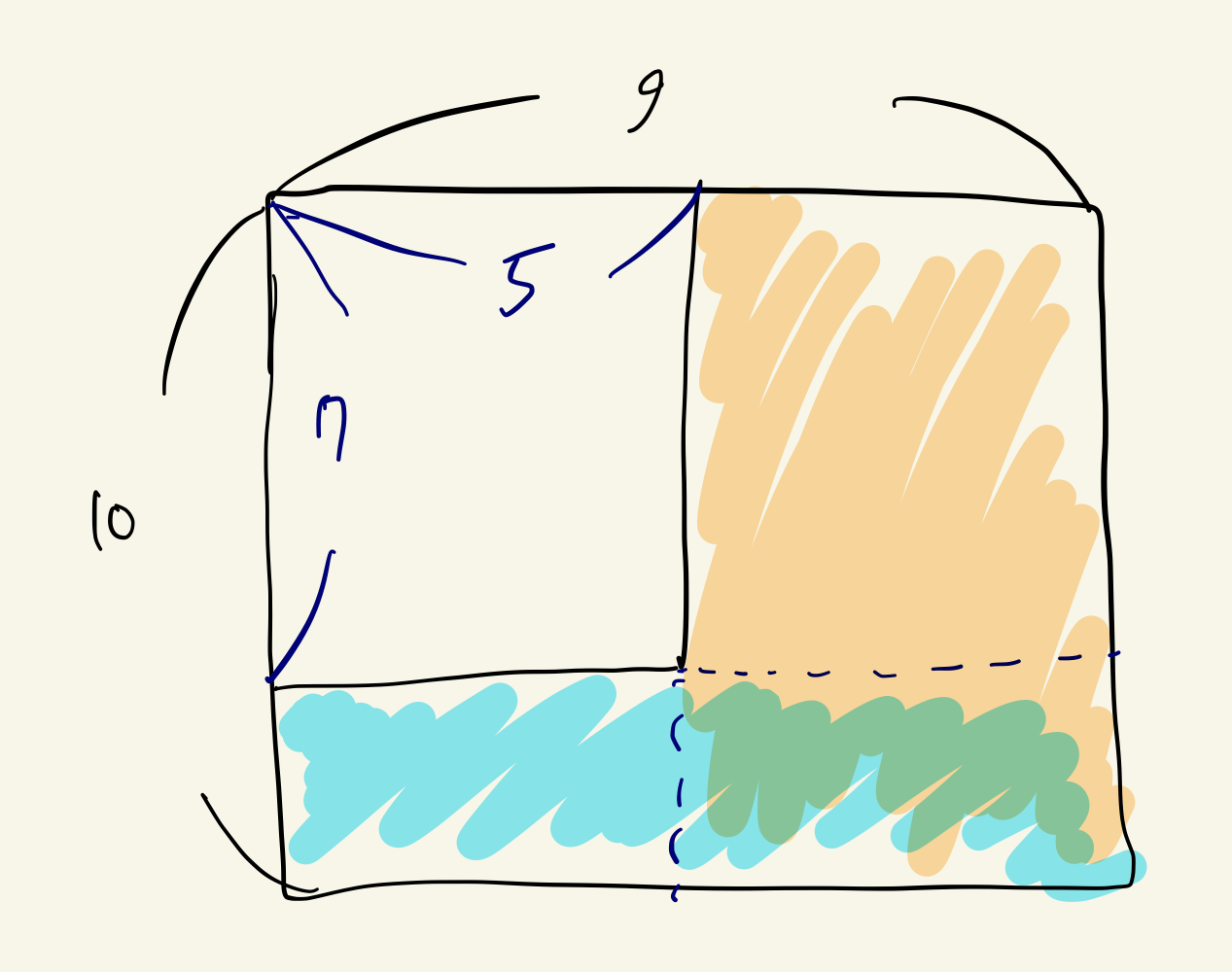
이렇게 구석에다가 두면 나머지 하나의 스티커를 둘 수 있는 두 개의 공간이 생긴다. (파란색, 황색으로 칠한 공간) 따라서 이 두 개의 공간에 나머지 하나의 스티커를 둘 수 있는지 판단하여, 둘 수 있다면 두 스티커의 넓이를 합하여 기존의 정답과 비교하면 된다.

소스 코드에서는 4개의 케이스로 나누었다. 그 이유는 스티커 각각을 회전할 수 있기 때문이다. 각 스티커에 대해 회전하지 않는 경우, 회전하는 경우 두 가지가 존재하므로 총 4가지 케이스로 나누어 최대값을 탐색하였다.

brute force인듯 하면서도 greedy라고 생각한 이유는, 우선 n개의 스티커 중 2개를 뽑아 모든 경우의 수를 탐색하는 것이고 각각의 경우에서 최대값을 greedy하게 탐색했기 때문이다. greedy한 생각이 들어가서 복잡도 또한 $O(100^2)$로, 상당히 작아진 것으로 분석된다.

[Source Code]

from itertools import combinations
h,w = map(int,input().split())
n = int(input())
s = []
ans = 0
for _ in range(n):
    r,c = map(int,input().split())
    s.append((r,c))
a = [[0]*w for _ in range(h)]
for c in combinations(s,2):
    (a,b),(x,y) = c
    cases = [((a,b),(x,y)), ((a,b),(y,x)), ((b,a),(x,y)), ((b,a),(y,x))]
    for case in cases:
        (a,b),(x,y) = case
        if a <= h and b <= w and x <= h and y <= w:
            # 정방향
            i,j = h-a,w
            k,l = h,w-b
            if (x <= i and y <= j) or (x <= k and y <= l):
                ans = max(ans, a*b + x*y)
print(ans)