[DL] Backpropagation
서울대학교 딥러닝 기초 강의를 듣고 정리하였다.
아래와 같은 fully connected neural network에서 backpropagation이 어떻게 진행되는지 수식을 통해 살펴보자.

notation을 정리해보자.
- $a_l$: $l$번째 layer에서 linear 연산을 적용한 값을 activation function에 넣은 neuron 값
- $a_l = f(z_l)$
- $a_1 = [a_{11} \; a_{12} \; a_{13} \; a_{14}]^T$
- $a_2 = [a_{21} \; a_{22} \; a_{23}]^T$
- $z_l$: $l$번째 layer에서 linear 연산을 적용한 값
- $z_{l+1} = W_l a_l + b_l$
- $z_1 = [z_{11} \; z_{12} \; z_{13} \; z_{14}]^T$
- $z_2 = [z_{21} \; z_{22} \; z_{23}]^T$
- $W_l$: $l$번째 layer의 weight matrix
- $ \begin{bmatrix} w_{11} & w_{12} & w_{13} & w_{14} \\ w_{21} & w_{22} & w_{23} & w_{24} \\ w_{31} & w_{32} & w_{33} & w_{34} \end{bmatrix} $
두번째 layer에서 linear 연산을 적용한 후의 neuron 값 $z_2$는 아래와 같이 표현할 수 있다.
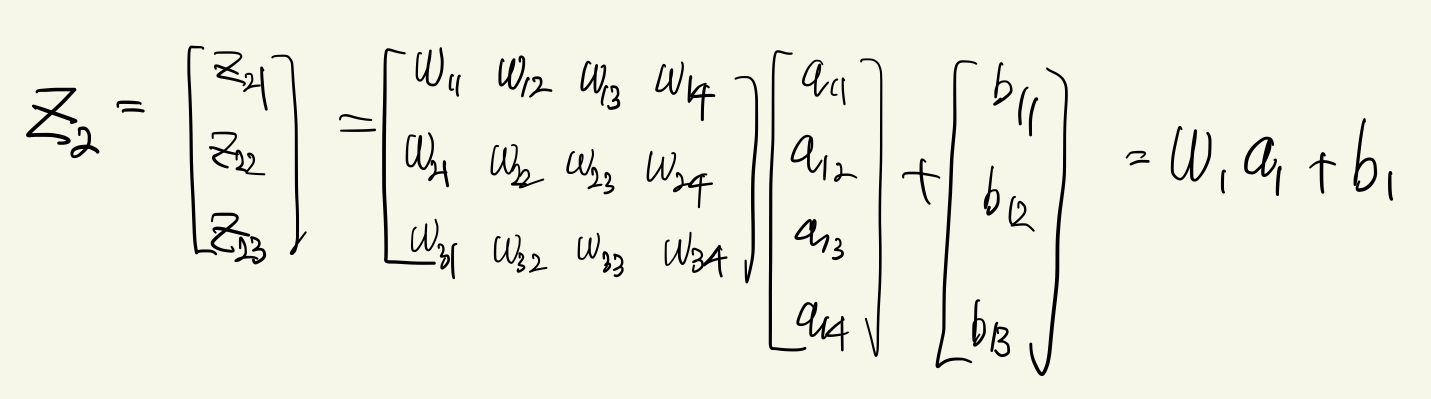
activation function을 적용한 후, 첫번째 layer의 최종 output neuron 값은 $a_1 = f(z_1)$이다. 이 식에서 $z_1$에 대해 backpropagation을 하면 아래와 같다.
\[ \dfrac{\partial L}{\partial z_1} = \dfrac{\partial L}{\partial a_1} \circ f'(z_1)\]
$\dfrac{\partial L}{\partial a_1}$을 어떻게 구해야할까? 위 식 $z_2 = W_1 a_1 + b_1$을 살펴보자. $a_1$에 행렬 $W_1$을 곱하고 bias term을 더한 것이 $z_2$이다. 따라서 직관적으로 $z_2$까지의 gradient에 $W_1$을 곱한 것이 $a_1$의 gradient임을 유추해볼 수 있다. 구체적으로 아래와 같다.

$a_1$의 gradient을 구했으니, $z_1$에 대한 gradient을 최종 정리해보자.
\[ \dfrac{\partial L}{\partial z_1} = W^T_1 \dfrac{\partial L}{\partial z_2} \circ f'(z_1)\]
이제 $W_1$의 gradient을 구해보자. 마찬가지로, $W_1$에 벡터 $a_1$을 곱하고 bias term을 더한 것이 $z_2$이다. 따라서 직관적으로 $z_2$까지의 gradient에 $a_1$을 곱한 것이 $W_1$의 gradient임을 유추해볼 수 있다. 구체적으로 아래와 같다.

마지막으로 bias term $b_1$의 gradient을 구해보자. 마찬가지로 $z_2 = W_1 a_1 + b_1$을 째려보자. $b_1$의 관점에서 보면, $z_2$의 gradient을 그대로 받는다. 따라서 아래와 같다.

정리하면 아래와 같다.
- $z_2 = W_1 a_1 + b_1$
- $a_1 = f(z_1)$
- 여기서 $z_1, W_1, a_1, b_1$에 대한 gradient을 구해본다.
- $\dfrac{\partial L}{\partial a_1} = W^T_1 \dfrac{\partial L}{\partial z_2}$
- $\delta_1 = \dfrac{\partial L}{\partial z_1} = \dfrac{\partial L}{\partial a_1} \circ f'(z_1) = W^T_1 \dfrac{\partial L}{\partial z_2} \circ f'(z_1)$
- $\dfrac{\partial L}{\partial W_1} = \delta_2 a_1^T$
- $\dfrac{\partial L}{\partial b_1} = \delta_2 $